题目内容
1.a是不为1的有理数,我们把$\frac{1}{1-a}$称为a的差倒数,如:2的差倒数是$\frac{1}{1-2}$=-1,-2的差倒数为$\frac{1}{1-(-2)}$=$\frac{1}{3}$.已知a1=-$\frac{1}{3}$,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数,…,依此类推.根据你对差倒数的理解完成下面问题:(1)a2=$\frac{3}{4}$,a3=4,a4=-$\frac{1}{3}$;
(2)通过(1)中的结果计算a2013的值.
分析 (1)把a1代入差倒数的关系式,计算出a2,a3,a4…,;
(2)由(1)得an+3=an,即{an}是一个周期为3的数列,再根据周期求解.
解答 解:(1)根据题设条件,由a1=-$\frac{1}{3}$得,
a2=$\frac{1}{1-(-\frac{1}{3})}$=$\frac{3}{4}$,
a3=$\frac{1}{1-\frac{3}{4}}$=4,
a4=$\frac{1}{1-4}$=-$\frac{1}{3}$=a1,
故答案为:$\frac{3}{4}$;4;-$\frac{1}{3}$.
(2)由(1)可知,an+3=an,
即{an}是一个周期为3的数列,
且前三项分别为:-$\frac{1}{3}$,$\frac{3}{4}$,4,数值周期往复,
因此,a2013=a670×3+3=a3=4.
点评 本题主要考查了探究数字的变化规律,理解差倒数的定义,涉及数列的周期性,属于中档题.

练习册系列答案
相关题目
17.化简$\sqrt{1-2sin(π+1)cos(π+1)}$等于( )
| A. | sin1-cos1 | B. | cos1-sin1 | C. | ±(sin1-cos1) | D. | sin1+cos1 |
13.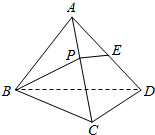 如图所示,在棱长为2的正四面体A-BCD中,E是棱AD的中点,若P是棱AC上一动点,则BP+PE的最小值为( )
如图所示,在棱长为2的正四面体A-BCD中,E是棱AD的中点,若P是棱AC上一动点,则BP+PE的最小值为( )
 如图所示,在棱长为2的正四面体A-BCD中,E是棱AD的中点,若P是棱AC上一动点,则BP+PE的最小值为( )
如图所示,在棱长为2的正四面体A-BCD中,E是棱AD的中点,若P是棱AC上一动点,则BP+PE的最小值为( )| A. | 3 | B. | $\sqrt{7}$ | C. | 1+$\sqrt{3}$ | D. | $\sqrt{5}$ |
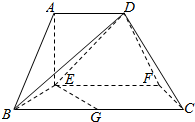 在如图所示的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2,AD=4,EF=3,AE=BE=2,G是BC的中点.
在如图所示的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2,AD=4,EF=3,AE=BE=2,G是BC的中点.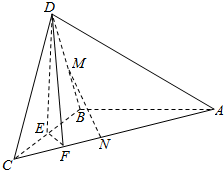 如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC点,F棱AC上,且AF=3FC.
如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC点,F棱AC上,且AF=3FC.