题目内容
18.已知三棱锥A-BCD中,点E,F分别是AB,CD的中点AC=BD=2,且直线AC,BD所成的角为60°,则线段EF的长度为( )| A. | 1 | B. | $\sqrt{2}$ | C. | 1或$\sqrt{2}$ | D. | 1或$\sqrt{3}$ |
分析 先确定BD、AC所成的角,再在三角形中,利用余弦定理,可求EF的长.
解答  解:取BC的中点G,连接EG、FG,则∠EGF(或其补角)为BD、AC所成的角,
解:取BC的中点G,连接EG、FG,则∠EGF(或其补角)为BD、AC所成的角,
∵BD、AC所成的角为60°,∴∠EGF=60°或120°
∵BD=AC=2,∴EG=FG=1,
∴∠EGF=60°时,EF=1;
∠EGF=120°时,EF=$\sqrt{1+1-2×1×1×cos120°}$=$\sqrt{3}$.
∴EF=1或EF=$\sqrt{3}$.
故选:D.
点评 本题考查空间角,考查学生的计算能力,正确确定BD、AC所成的角是关键,解题时要注意余弦定理的合理运用..

练习册系列答案
相关题目
14.已知f(x)=$\left\{\begin{array}{l}{0,x>0}\\{1,x=0}\\{2x-1,x<0}\end{array}\right.$,则f(f[f(6)])的值是( )
| A. | 0 | B. | 1 | C. | -1 | D. | 3 |
13.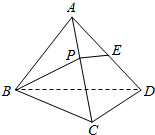 如图所示,在棱长为2的正四面体A-BCD中,E是棱AD的中点,若P是棱AC上一动点,则BP+PE的最小值为( )
如图所示,在棱长为2的正四面体A-BCD中,E是棱AD的中点,若P是棱AC上一动点,则BP+PE的最小值为( )
 如图所示,在棱长为2的正四面体A-BCD中,E是棱AD的中点,若P是棱AC上一动点,则BP+PE的最小值为( )
如图所示,在棱长为2的正四面体A-BCD中,E是棱AD的中点,若P是棱AC上一动点,则BP+PE的最小值为( )| A. | 3 | B. | $\sqrt{7}$ | C. | 1+$\sqrt{3}$ | D. | $\sqrt{5}$ |
7.一个多边形的内角中,有3个直角,4个钝角,则这个多边形的边数最多是( )
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
8.在△ABC中,角A、B、C所对边分别为a、b、c,若asinB=2bsinAcosC,则角C的大小为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
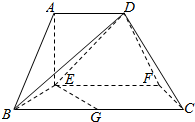 在如图所示的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2,AD=4,EF=3,AE=BE=2,G是BC的中点.
在如图所示的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2,AD=4,EF=3,AE=BE=2,G是BC的中点.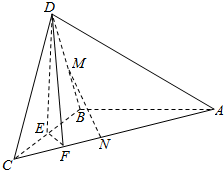 如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC点,F棱AC上,且AF=3FC.
如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC点,F棱AC上,且AF=3FC.