题目内容
11．
如图，在三棱锥V-ABC中，VA=VB=VC=4，∠AVB=∠AVC=∠BVC=30°，过点A作截面△AEF，求△AEF周长的最小值．
分析 沿着侧棱VA把正三棱锥V-ABC展开在一个平面内，如图，则AA′即为△AEF周长的最小值，在△VAA′k，由勾股定理能求出AA′的值．
解答 解：如图，沿着侧棱VA把正三棱锥V-ABC展开在一个平面内，如图（2），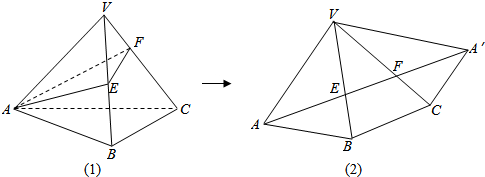
则AA′即为△AEF的周长的最小值，
且∠AVA′=3×30°=90°，
△VAA′中，由勾股定理得：
AA′=$\sqrt{V{A}^{2}+（V{A}^{'}）^{2}}$=$\sqrt{16+16}$=4$\sqrt{2}$．
点评 本题考查正三棱锥中截面三角形周长的最小值的求法，是中档题，解题时要认真审题，注意棱锥的侧面展开图研究线段的最小值问题的合理运用．
练习册系列答案
相关题目
7．不等式-3x2＜0的解集为（ ）
| A． | ∅ | B． | R | C． | （-∞，0）∪（0，+∞） | D． | （-$\sqrt{3}$，$\sqrt{3}$） |
如图，在三棱锥D-ABC中，已知△BCD是正三角形，AB⊥平面BCD，AB=BC=a，E为BC点，F棱AC上，且AF=3FC．