题目内容
14.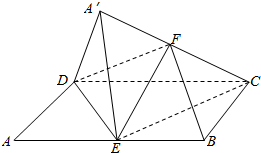 如图,在平行四边形ABCD中,AB=2BC,∠ABC=120°.E为线段AB的中点,将△ADE沿直线DE翻折成△A′DE,使面A′DE⊥平面BCD,F为线段A′C的中点.
如图,在平行四边形ABCD中,AB=2BC,∠ABC=120°.E为线段AB的中点,将△ADE沿直线DE翻折成△A′DE,使面A′DE⊥平面BCD,F为线段A′C的中点.(Ⅰ)求证:BF∥面A′DE;
(Ⅱ)求证:CE⊥平面A′DE
(Ⅲ)若BC=2,求三棱锥A′-DEF的体积.
分析 (Ⅰ)延长CB交DE于点G,连接A'G,证明FB∥A'G,即可证明BF∥面A′DE;
(Ⅱ)证明CE⊥DE,利用面A'DE⊥面CDE,证明CE⊥平面A′DE
(Ⅲ)取A′E的中点N,连接FN,证明FN是三棱锥F-A′DE的高,即可求三棱锥A′-DEF的体积.
解答  (I)证明:延长CB交DE于点G,连接A'G,
(I)证明:延长CB交DE于点G,连接A'G,
在△GDC中,E为AB中点,且EB∥DC,所以B为GC中点.
在△A'GC中,F为A'C中点,B为GC中点,
所以FB∥A'G.
因为FB?面A'DE,A'G?面A'DE,所以FB∥面A'DE…(4分)
(II)证明:在平行四边形ABCD中,AB=2BC=4,
因为∠ABC=120°,
所以∠DAE=60°,且DE=AD=AE=EB=BC=2,
所以∠DEA=∠DAE=60°,∠BEC=∠ECB=30°,
所以∠DEC=90°,即CE⊥DE,…(6分)
因为面A'DE⊥面CDE,所以CE⊥平面A′DE…(7分)
(III)解:取A′E的中点N,连接FN,
由F为线段B的中点,得FN是C的中位线,所以FN∥CE,所以FN⊥平面A′DE,
即FN是三棱锥F-A′DE的高.…(8分)
在△EBC中,EB=BC=2,∠ABC=120°,由余弦定理得EC=2$\sqrt{3}$,所以FN=$\sqrt{3}$
S△ADE=S△A′DE=$\frac{1}{2}×DA×DE×sin60°$=$\sqrt{3}$,
所以三棱锥A′-DEF的体积V=$\frac{1}{3}×\sqrt{3}×\sqrt{3}$=1.…(12分)
点评 本题考查线面平行、垂直的判定,考查三棱锥A′-DEF的体积,同时考查空间想象能力和推理论证能力,属于中档题.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
10.已知θ∈R,且sinθ-2cosθ=$\sqrt{5}$,则tan2θ=( )
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | -$\frac{3}{4}$ | D. | -$\frac{4}{3}$ |
4.函数y=lg(1+x)-lg(1-x)的图象( )
| A. | 关于原点对称 | B. | 关于直线y=-x对称 | ||
| C. | 关于y轴对称 | D. | 关于直线y=x对称 |
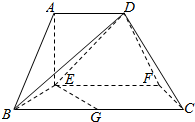 在如图所示的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2,AD=4,EF=3,AE=BE=2,G是BC的中点.
在如图所示的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2,AD=4,EF=3,AE=BE=2,G是BC的中点.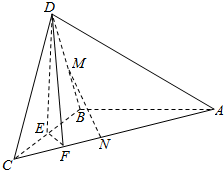 如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC点,F棱AC上,且AF=3FC.
如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC点,F棱AC上,且AF=3FC.