题目内容
【题目】设
是等差数列，公差为
，前
项和为
.
（1）设
，
，求的最大值.
（2）设
，
，数列
的前项和为
，且对任意的
，都有
，求的取值范围.
【答案】（1）2020（2）
【解析】
（1）运用等差数列的通项公式可得公差d，再由等差数列的求和公式，结合配方法和二次函数的最值求法，可得最大值；
（2）由题意可得数列{bn}为首项为2，公比为2d的等比数列，讨论d＝0，d＞0，d＜0，判断数列{bn}的单调性和求和公式，及范围，结合不等式恒成立问题解法，解不等式可得所求范围．
（1）a1＝40，a6＝38，可得d
，
可得Sn＝40n
n（n﹣1）
（n
）2
，
由n为正整数，可得n＝100或101时，Sn取得最大值2020；
（2）设
，数列{bn}的前n项和为Tn，
可得an＝1+（n﹣1）d，数列{bn}为首项为2，公比为2d的等比数列，
若d＝0，可得bn＝2；d＞0，可得{bn}为递增数列，无最大值；
当d＜0时，Tn
，
对任意的n∈N*，都有Tn≤20，可得20
，且d＜0，
解得d≤
．
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
快乐暑假暑假能力自测中西书局系列答案
【题目】某人某天的工作是：驾车从
地出发，到
两地办事，最后返回地，
三地之间各路段行驶时间及当天降水概率如下表：
路段 | 正常行驶所需时间（小时） | 上午降水概率 | 下午降水概率 |
| 2 | 0.3 | 0.6 |
| 2 | 0.2 | 0.7 |
| 3 | 0.3 | 0.9 |
若在某路段遇到降水，则在该路段行驶的时间需延长1小时.
现有如下两个方案：
方案甲：上午从地出发到
地办事，然后到达
地， 下午在地办事后返回地；
方案乙：上午从地出发到地办事，下午从
地出发到达地，办事后返回地.设此人8点从地出发，在各地办事及午餐的累积时间为2小时.
现采用随机数表法获取随机数并进行随机模拟试验，按照以下随机数表，以方框内的数字5为起点，从左向右依次读取数据，若到达某行最后一个数字，则从下一行最左侧数字继续读取，每次读取4位随机数，第1位数表示采取的方案，其中0-4表示采用方案甲，5-9表示采用方案乙；第2-4位依次分别表示当天行驶的三个路段上是否降水，若某路段降水概率为
，则
表示降水，
表示不降水.（符号
表示的数集包含
）
05 26 93 70 60 22 35 85 15 13 92 03 51 59 77 59 56 78 06 83 52 91 05 70 74
07 97 10 88 23099842 99 64 61 71 6299 15 06
1 29 169358 05 77 05 91
51 26 87 85 85 54 87 66 47 54 73 32 08 11 12 44 95 92 63 16 29 56 24 29 48
26 99 61 65 53 58 37 78 80 70 42 10 50 67 42 32 17 55 85 74 94 44 67 16 94
14 65 52 68 75 87 59 36 22 41 26 78 63 06 55 13 08 27 01 50 15 29 39 39 43
（1）利用数据“5129”模拟当天的情况，试推算他当日办完事返回地的时间；
（2）利用随机数表依次取出采用甲、乙方案的模拟结果各两组，分别计算甲、乙两个方案的平均时间，并回答哪个方案办完事后能尽早返回地.
【题目】2019年10月1日是新中国的第70个国庆日，庄重的阅兵、欢乐的游行、热烈的联欢尽显祖国的繁荣昌盛.为了了解当天某校900名高三学生的观看情况，从中抽取了100名学生，情况如下表所示：
观看情况 | 电视观看 | 网络观看 | 没有观看 |
人数 | 35 | 60 | 5 |
新时代下，网络观看使用最多的是手机，其它还有电脑、ipad等.“是否使用手机观看”与“学生的性别”之间对应的列联表如下：
使用手机观看 | 其它方式观看 | 合计 | |
男学生 | 20 | 8 | 28 |
女学生 | 20 | 12 | 32 |
合计 | 40 | 20 | 60 |
（1）估计该校高三学生当天的观看人数.
（2）当天没有观看的5名学生中，有3人第二天观看了重播.从这5名学生中任选2人求这2人第二天都看了重播的概率；
（3）根据列联表判断，能否有95%的把握认为网络观看的学生中“是否使用手机观看”与“学生的性别”有关？
附：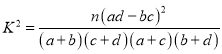
，其中
.
| 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
