题目内容
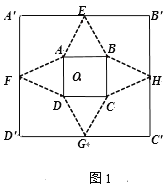
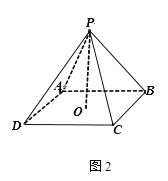
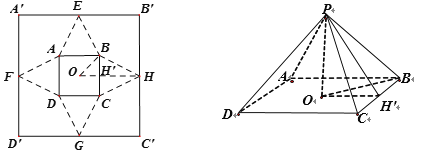
【题目】如图1,已知正方形铁片![]() 边长为2a米,四边中点分别为E,F,G,H,沿着虚线剪去大正方形的四个角,剩余为四个全等的等腰三角形和一个正方形ABCD(两个正方形中心重合且四边相互平行),沿正方形ABCD的四边折起,使E,F,G,H四点重合,记为P点,如图2,恰好能做成一个正四棱锥(粘贴损耗不计),PO⊥底面ABCD,O为正四棱锥底面中心,设正方形ABCD的边长为2x米.
边长为2a米,四边中点分别为E,F,G,H,沿着虚线剪去大正方形的四个角,剩余为四个全等的等腰三角形和一个正方形ABCD(两个正方形中心重合且四边相互平行),沿正方形ABCD的四边折起,使E,F,G,H四点重合,记为P点,如图2,恰好能做成一个正四棱锥(粘贴损耗不计),PO⊥底面ABCD,O为正四棱锥底面中心,设正方形ABCD的边长为2x米.
(1)若正四棱锥的棱长都相等,求所围成的正四棱锥的全面积S;
(2)请写出正四棱锥的体积V关于x的函数,并求V的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
. ![]() .
.
【解析】
(1)连接OH交BC于点H′,由正方形ABCD边长为2x,所以HH′=a-x.
可得![]() 的长及
的长及![]() 的长,由
的长,由![]() 得可得
得可得![]() 的值,可得正四棱锥的全面积
的值,可得正四棱锥的全面积![]() ,计算可得答案;
,计算可得答案;
(2)可得![]() ,可得
,可得![]() 关于
关于![]() 的函数,对其求导,利用导数可得V的最大值.
的函数,对其求导,利用导数可得V的最大值.
解:在图1中连接OH交BC于点H′,
因为正方形ABCD边长为2x,所以HH′=a-x.
在图2中,OH′=x,PH′=a-x,
由勾股定理得,正四棱锥的高
![]()
![]() .
.
(1)在直角三角形![]() 中,
中,![]() ,
,
所以![]() ,
,
由![]() 得,
得,![]() ,
,
整理得,![]() ,解得
,解得![]() (
(![]() 舍去).
舍去).
所以,正四棱锥的全面积![]()
![]()
![]() 平方米.
平方米.
(2)![]() ,
,
所以![]() .
.
因为![]() ,设
,设![]() ,
,
则![]()
![]() ,
,
令![]() 得,
得,![]() ,当
,当![]() 时,
时,![]() ,
,![]() 在区间
在区间![]() 上递增;
上递增;
当![]() 时,
时,![]() ,
,![]() 在区间
在区间![]() 上递减.
上递减.
所以当![]() 时,
时,![]() 取得最大值,此时
取得最大值,此时![]() 立方米.
立方米.

【题目】我们把活跃网店数量较多的村庄称为淘宝村,随着电子商务在中国的发展,不少农村出现了一批专业的淘宝村,已知某乡镇有多个淘宝村,现从该乡镇淘宝村中随机抽取![]() 家商户,统计他们某一周的销售收入,结果统计如下:
家商户,统计他们某一周的销售收入,结果统计如下:
销售收入(收入) |
|
|
|
|
商户数 |
|
|
|
|
(1)从这![]() 家商户中按该周销售收入超过
家商户中按该周销售收入超过![]() 万元与不超过
万元与不超过![]() 万元分为
万元分为![]() 组,按分层抽样从中抽取
组,按分层抽样从中抽取![]() 家参加经验交流会,并从这
家参加经验交流会,并从这![]() 家中选
家中选![]() 家进行发言,求选出的
家进行发言,求选出的![]() 家恰有
家恰有![]() 家销售收入超过
家销售收入超过![]() 万元的概率;
万元的概率;
(2)若这![]() 家商户中有
家商户中有![]() 家商户入驻两家网购平台,其中
家商户入驻两家网购平台,其中![]() 家销售收入高于
家销售收入高于![]() 万元,完成下面的
万元,完成下面的![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为“销售收入是否高于
的把握认为“销售收入是否高于![]() 万元与入驻两家网购平台有关”?
万元与入驻两家网购平台有关”?
入驻两家网购平台 | 仅入驻一家网购平台 | 合计 | |
销售收入高于 | |||
销售收入不高于 | |||
合计 |
附: .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
【题目】某快递公司收取快递费用的标准是:重量不超过![]() 的包裹收费
的包裹收费![]() 元;重量超过
元;重量超过![]() 的包裹,除
的包裹,除![]() 收费
收费![]() 元之外,超过
元之外,超过![]() 的部分,每超出
的部分,每超出![]() (不足
(不足![]() ,按
,按![]() 计算)需再收
计算)需再收![]() 元.该公司将最近承揽的
元.该公司将最近承揽的![]() 件包裹的重量统计如下:
件包裹的重量统计如下:
包裹重量(单位: |
|
|
|
|
|
包裹件数 |
|
|
|
|
|
公司对近![]() 天,每天揽件数量统计如下表:
天,每天揽件数量统计如下表:
包裹件数范围 |
|
|
|
|
|
包裹件数 (近似处理) |
|
|
|
|
|
天数 |
|
|
|
|
|
以上数据已做近似处理,并将频率视为概率.
(1)计算该公司未来![]() 天内恰有
天内恰有![]() 天揽件数在
天揽件数在![]() 之间的概率;
之间的概率;
(2)(i)估计该公司对每件包裹收取的快递费的平均值;
(ii)公司将快递费的三分之一作为前台工作人员的工资和公司利润,剩余的用作其他费用.目前前台有工作人员![]() 人,每人每天揽件不超过
人,每人每天揽件不超过![]() 件,工资
件,工资![]() 元.公司正在考虑是否将前台工作人员裁减
元.公司正在考虑是否将前台工作人员裁减![]() 人,试计算裁员前后公司每日利润的数学期望,并判断裁员是否对提高公司利润更有利?
人,试计算裁员前后公司每日利润的数学期望,并判断裁员是否对提高公司利润更有利?