题目内容
【题目】已知圆![]() ,直线
,直线![]() ,
,![]() 为任意实数.
为任意实数.
(1)求证:直线![]() 必与圆
必与圆![]() 相交;
相交;
(2)![]() 为何值时,直线
为何值时,直线![]() 被圆
被圆![]() 截得的弦长
截得的弦长![]() 最短?最短弦长是多少?
最短?最短弦长是多少?
(3)若直线![]() 被圆
被圆![]() 截得的弦
截得的弦![]() 的中点为点
的中点为点![]() ,求点
,求点![]() 的轨迹方程.
的轨迹方程.
【答案】(1)见解析(2)![]() ,最短弦长为
,最短弦长为![]() (3)
(3)![]()
【解析】
(1)通过直线![]() 转化为直线系,求出直线恒过的定点,判断定点与圆的位置故选即可判断直线
转化为直线系,求出直线恒过的定点,判断定点与圆的位置故选即可判断直线![]() 与圆C相交;(2)说明直线|被圆C截得的弦长最小时,圆心与定点连线与直线
与圆C相交;(2)说明直线|被圆C截得的弦长最小时,圆心与定点连线与直线![]() 垂直,求出斜率即可求出
垂直,求出斜率即可求出![]() 的值,再由勾股定理即可得到最短弦长;(3)由
的值,再由勾股定理即可得到最短弦长;(3)由![]() 得弦
得弦![]() 的中点
的中点![]() 的轨迹方程.
的轨迹方程.
(1)由![]() ,
,
得![]() ,
,
![]() ,
,
![]() ,得
,得![]() ,
,
![]() 直线
直线![]() 恒过点
恒过点![]() ,又圆
,又圆![]() ,半径为
,半径为![]() ,
,
![]() ,
,
![]() 在圆内,则直线
在圆内,则直线![]() 必与圆
必与圆![]() 相交.
相交.
(2)由(1)知![]() 在圆内,当直线
在圆内,当直线![]() 被圆
被圆![]() 截得的弦长
截得的弦长![]() 最短时,
最短时,![]() ,
,
又![]() ,
,
则直线![]() 的斜率为
的斜率为![]() ,即有
,即有![]() ,解得
,解得![]() .
.
此时最短弦长为![]() .
.
故![]() 时,直线
时,直线![]() 被圆
被圆![]() 截得的弦长
截得的弦长![]() 最短,最短弦长是
最短,最短弦长是![]() .
.
(3)设![]() ,又
,又![]() 为
为![]() 的中点,
的中点,
![]() ,
,![]() ,
,
可得![]() .
.
![]() ,
,
即![]() .
.

【题目】近几年一种新奇水果深受广大消费者的喜爱,一位农户发挥聪明才智,把这种露天种植的新奇水果搬到了大棚里,收到了很好的经济效益.根据资料显示,产出的新奇水果的箱数x(单位:十箱)与成本y(单位:千元)的关系如下:
x | 1 | 3 | 4 | 6 | 7 |
y | 5 | 6.5 | 7 | 7.5 | 8 |
y与x可用回归方程![]() (其中
(其中![]() ,
,![]() 为常数)进行模拟.
为常数)进行模拟.
(1)若该农户产出的该新奇水果的价格为150元/箱,试预测该新奇水果100箱的利润是多少元.(利润=售价-成本)
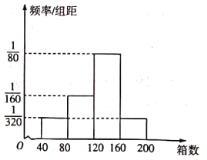
(2)据统计,10月份的连续16天中该农户每天为甲地可配送的该新奇水果的箱数的频率分布直方图如图,用这16天的情况来估计相应的概率.一个运输户拟购置n辆小货车专门运输该农户为甲地配送的该新奇水果,一辆货车每天只能运营一趟,每辆车每趟最多只能装载40箱该新奇水果,满载发车,否则不发车.若发车,则每辆车每趟可获利500元,若未发车,则每辆车每天平均亏损200元试比较![]() 和
和![]() 时此项业务每天的利润平均值的大小.
时此项业务每天的利润平均值的大小.
参考数据与公式:设![]() ,则
,则
|
|
|
|
0.54 | 6.8 | 1.53 | 0.45 |
线性回归直线![]() 中,
中, ,
,![]() .
.