题目内容
【题目】已知椭圆![]() :
:![]() 过点
过点![]() ,且它的焦距是短轴长的
,且它的焦距是短轴长的![]() 倍.
倍.
(1)求椭圆![]() 的方程.
的方程.
(2)若![]() ,
,![]() 是椭圆
是椭圆![]() 上的两个动点(
上的两个动点(![]() ,
,![]() 两点不关于
两点不关于![]() 轴对称),
轴对称),![]() 为坐标原点,
为坐标原点,![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,问是否存在非零常数
,问是否存在非零常数![]() ,使当
,使当![]() 时,
时,![]() 的面积
的面积![]() 为定值?若存在,求
为定值?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)存在这样的常数
;(2)存在这样的常数![]() ,此时
,此时![]() .
.
【解析】
(1)将点![]() 的坐标代入椭圆方程,结合
的坐标代入椭圆方程,结合![]() 和
和![]() 列方程组,解方程组求得椭圆的标准方程.(2)设直线
列方程组,解方程组求得椭圆的标准方程.(2)设直线![]() 的方程为
的方程为![]() 和
和![]() 两点的坐标,将
两点的坐标,将![]() 两点两点坐标代入
两点两点坐标代入![]() ,化简得到
,化简得到![]() ①.联立直线
①.联立直线![]() 的方程和椭圆方程,写出韦达定理,利用点到直线距离公式和弦长公式求得三角形
的方程和椭圆方程,写出韦达定理,利用点到直线距离公式和弦长公式求得三角形![]() 的面积的表达式,结合①解得
的面积的表达式,结合①解得![]() 和
和![]() 的值.
的值.
解:(1)因为椭圆![]() :
:![]() 过点
过点![]() ,
,
所以![]() ,
,
又因为该椭圆的焦距是短轴长的![]() 倍,所以
倍,所以![]() ,从而
,从而![]() .
.
联立方程组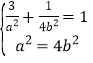 ,解得
,解得![]() ,所以
,所以![]() .
.
(2)设存在这样的常数![]() ,使
,使![]() ,
,![]() 的面积
的面积![]() 为定值.设直线
为定值.设直线![]() 的方程为
的方程为![]() ,点
,点![]() ,点
,点![]() ,则由
,则由![]() 知
知![]() ,
,![]() ,所以
,所以![]() .①
.①
联立方程组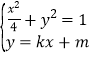 ,消去
,消去![]() 得
得![]() .
.
所以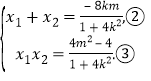 ,
,
点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
![]() 的面积
的面积![]() .④
.④
将②③代入①得![]() ,
,
化简得![]() ,⑤
,⑤
将⑤代入④得![]()
![]() ,
,
要使上式为定值,只需![]() ,
,
即需![]() ,从而
,从而![]() ,此时
,此时![]() ,
,![]() ,
,
所以存在这样的常数![]() ,此时
,此时![]() .
.

练习册系列答案
相关题目