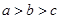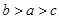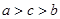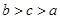题目内容
定义新运算⊕：当a≥b时，a⊕b＝a；当a<b时，a⊕b＝b2，则函数f(x)＝(1⊕x)x－(2⊕x)，x∈[－2,2]的最大值等于________．
6
由已知得当－2≤x≤1时，
f(x)＝x－2，
当1<x≤2时，f(x)＝x3－2.
∵f(x)＝x－2，f(x)＝x3－2在定义域内都为增函数．
∴f(x)的最大值为f(2)＝23－2＝6.
f(x)＝x－2，
当1<x≤2时，f(x)＝x3－2.
∵f(x)＝x－2，f(x)＝x3－2在定义域内都为增函数．
∴f(x)的最大值为f(2)＝23－2＝6.
练习册系列答案
相关题目
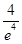
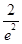
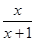)<f(－
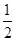)的解集为________．
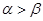，则下列结论正确的是( )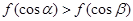
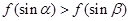
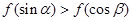
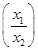＝f(x1)－f(x2)，且当x>1时，f(x)<0.
（
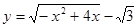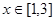）的图象绕坐标原点逆时针旋转
（
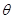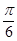
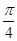
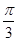
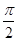
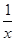
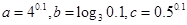，则（ ）
