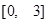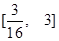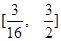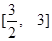题目内容
已知定义在区间(0，＋∞)上的函数f(x)满足f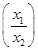
＝f(x1)－f(x2)，且当x>1时，f(x)<0.
(1)求f(1)的值；
(2)判断f(x)的单调性；
(3)若f(3)＝－1，求f(x)在[2,9]上的最小值．
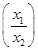＝f(x1)－f(x2)，且当x>1时，f(x)<0.(1)求f(1)的值；
(2)判断f(x)的单调性；
(3)若f(3)＝－1，求f(x)在[2,9]上的最小值．
（1）0 （2）函数f(x)在区间(0，＋∞)上是单调递减函数． （3）－2
解：(1)令x1＝x2>0，
代入得f(1)＝f(x1)－f(x1)＝0，
故f(1)＝0.
(2)任取x1，x2∈(0，＋∞)，且x1>x2，
则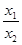
>1，由于当x>1时，f(x)<0，
所以f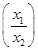<0，即f(x1)－f(x2)<0，
因此f(x1)<f(x2)，
所以函数f(x)在区间(0，＋∞)上是单调递减函数．
(3)∵f(x)在(0，＋∞)上是单调递减函数．
∴f(x)在[2,9]上的最小值为f(9)．
由f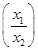＝f(x1)－f(x2)得，
f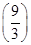
＝f(9)－f(3)，
而f(3)＝－1，∴f(9)＝－2.
∴f(x)在[2,9]上的最小值为－2.
代入得f(1)＝f(x1)－f(x1)＝0，
故f(1)＝0.
(2)任取x1，x2∈(0，＋∞)，且x1>x2，
则
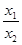>1，由于当x>1时，f(x)<0，所以f
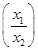<0，即f(x1)－f(x2)<0，因此f(x1)<f(x2)，
所以函数f(x)在区间(0，＋∞)上是单调递减函数．
(3)∵f(x)在(0，＋∞)上是单调递减函数．
∴f(x)在[2,9]上的最小值为f(9)．
由f
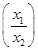＝f(x1)－f(x2)得，f
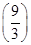＝f(9)－f(3)，而f(3)＝－1，∴f(9)＝－2.
∴f(x)在[2,9]上的最小值为－2.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
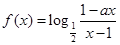为奇函数，
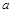为常数．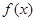
在区间（1，＋∞）内单调递增；
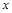的值，不等式
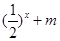恒成立，求实数
的取值范围．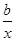
在(0，＋∞)上都是减函数，则y＝ax2＋bx在(0，＋∞)上( )
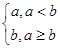，函数f(x)＝min{
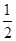x，－|x－1|＋2}(x∈R)的最大值为________．
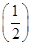1－x，则：
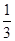)的x的取值范围是( )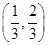
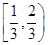
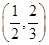
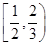
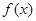在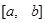
上的最大值和最小值分别为
、
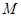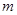，那么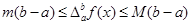
.根据这一结论求出
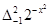的取值范围（ ）.
