题目内容
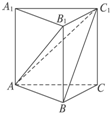
如图,在棱长为a的正方体A1B1C1D1-ABCD中,
(1)作出面A1BC1与面ABCD的交线l,判断l与直线A1C1位置关系,并给出证明;
(2)证明B1D⊥面A1BC1;
(3)求直线AC到面A1BC1的距离;
(4)若以A为坐标原点,分别以AB,AD,AA1所在的直线为x轴、y轴、z轴,建立空间直角坐标系,试写出C,C1两点的坐标.

(1)作出面A1BC1与面ABCD的交线l,判断l与直线A1C1位置关系,并给出证明;
(2)证明B1D⊥面A1BC1;
(3)求直线AC到面A1BC1的距离;
(4)若以A为坐标原点,分别以AB,AD,AA1所在的直线为x轴、y轴、z轴,建立空间直角坐标系,试写出C,C1两点的坐标.

(1)在平面ABCD内过点B作AC的平行线BE,
∵AC∥A1C1,AC∥BE,
∴BE∥A1C1,
∴面A1BC1与面ABCD的交线l与BE重合,
即直线BE就是所求的直线l.
∵BE∥A1C1,
l与BE重合,
∴l∥A1C1.
(2)证明:连接B1D1,
∵A1B1C1D1是正方形,
∴A1C1⊥B1D1,
∵A1C1⊥DD1,
∴A1C1⊥面DBB1D1,
∴A1C1⊥B1D.
同理A1B⊥面ADC1B1,
∴A1B⊥B1D,
∵A1C1∩A1B=A1,
∴B1D⊥面A1BC1.
(3)∵AC∥A1C1,且AC在面A1BC1外,A1C1?面A1BC1,
∴AC∥面A1BC1,
∴直线AC到面A1BC1的距离即为点A到面A1BC1的距离,记为h,
在三棱锥中A-A1BC1中,
VA_A1BC1=VC1-ABA1,
∵正方体A1B1C1D1-ABCD棱长为a,
∴VA-A1BC1=
•S△A1BC1•h=
×
×(
a)2×h×sin60°=
h,
VC1-ABA1=
•S△ABA1•A1C1=
•
•a•a•
a=
a3,
∵VA_A1BC1=VC1-ABA1,
∴h=
a.
(4)若以A为坐标原点,
分别以AB,AD,AA1所在的直线为x轴、y轴、z轴,
建立如图所示的空间直角坐标系,
∵正方体A1B1C1D1-ABCD的棱长为a,
∴C(a,a,0),C1(a,a,a).

∵AC∥A1C1,AC∥BE,
∴BE∥A1C1,
∴面A1BC1与面ABCD的交线l与BE重合,
即直线BE就是所求的直线l.
∵BE∥A1C1,
l与BE重合,
∴l∥A1C1.
(2)证明:连接B1D1,
∵A1B1C1D1是正方形,
∴A1C1⊥B1D1,
∵A1C1⊥DD1,
∴A1C1⊥面DBB1D1,
∴A1C1⊥B1D.
同理A1B⊥面ADC1B1,
∴A1B⊥B1D,
∵A1C1∩A1B=A1,
∴B1D⊥面A1BC1.
(3)∵AC∥A1C1,且AC在面A1BC1外,A1C1?面A1BC1,
∴AC∥面A1BC1,
∴直线AC到面A1BC1的距离即为点A到面A1BC1的距离,记为h,
在三棱锥中A-A1BC1中,
VA_A1BC1=VC1-ABA1,
∵正方体A1B1C1D1-ABCD棱长为a,
∴VA-A1BC1=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| ||
| 6 |
VC1-ABA1=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| ||
| 6 |
∵VA_A1BC1=VC1-ABA1,
∴h=
| ||
| 3 |
(4)若以A为坐标原点,
分别以AB,AD,AA1所在的直线为x轴、y轴、z轴,
建立如图所示的空间直角坐标系,
∵正方体A1B1C1D1-ABCD的棱长为a,
∴C(a,a,0),C1(a,a,a).


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目