题目内容
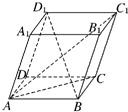
二面角α-l-β为60°,A、B是棱l上的两点,AC、BD分别在半平面α、β内,
AC⊥l,BD⊥l,且AB=AC=a,BD=2a,则CD的长为( )
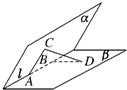
AC⊥l,BD⊥l,且AB=AC=a,BD=2a,则CD的长为( )
| A.2a | B.
| C.a | D.
|

∵AC⊥l,BD⊥l,
∴<
,
>=60°,且
•
=0,
•
=0,
∴
=
+
+
,
∴|
|=
=
=2a.
答案:A
∴<
| AC |
| BD |
| AC |
| BA |
| AB |
| BD |
∴
| CD |
| CA |
| AB |
| BD |
∴|
| CD |
(
|
=
| a2+a2+(2a)2+2a•2acos120° |
答案:A


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目