题目内容
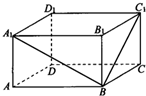
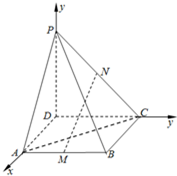
如图，P是正方形ABCD所在平面外一点，且PD⊥AD，PD⊥DC，PD=3，AD=2，若M、N分别是AB、PC的中点．
（1）求证：MN⊥DC；
（2）求点M到平面PAC的距离．
（1）求证：MN⊥DC；
（2）求点M到平面PAC的距离．
（本小题满分13分）
如图建系，则D（0，0，0），
A（2，0，0），B（2，2，0），C（0，2，0），P（0，0，3），则M(2，1，0)，N(0，1，
)．
（1）∴
=(-2，0，
)，
=(0，2，0)∴
•
=(-2，0，
)•(0，2，0)=0，∴MN⊥DC．
（2）设
=(x，y，z)为平面PAC的一个法向量，
=(2，0，-3)，
=(0，2，-3)，
由
，得
取x=3，则y=3，z=2，
=(3，3，2)，
=(-1，0，0)
∴d=
=
=
，
∴点M到平面PAC的距离为
．
如图建系，则D（0，0，0），
A（2，0，0），B（2，2，0），C（0，2，0），P（0，0，3），则M(2，1，0)，N(0，1，
| 3 |
| 2 |
（1）∴
| MN |
| 3 |
| 2 |
| DC |
| MN |
| DC |
| 3 |
| 2 |
（2）设
| n |
| PA |
| PC |
由
|
|
取x=3，则y=3，z=2，
| n |
| MA |
∴d=
|
| ||||
|
|
| 3 | ||
|
3
| ||
| 22 |
∴点M到平面PAC的距离为
3
| ||
| 22 |
练习册系列答案
教学练新同步练习系列答案
课前课后同步练习系列答案
课堂小作业系列答案
黄冈小状元口算速算练习册系列答案
相关题目
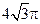的球的表面上有A，B，C三点，AB=1，BC=
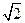，A，C两点的球面距离为
，则球心到平面ABC的距离为_________．
