题目内容
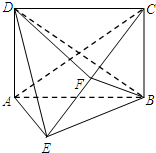
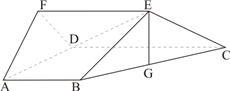
如图,面SAB⊥矩形ABCD所在的平面,△SAB是正三角形,F、E分别是SD,BC的中点.
(1)求证:EF∥平面SAB;
(2)求证:EF⊥AD.

(1)求证:EF∥平面SAB;
(2)求证:EF⊥AD.

证明:(1)如图所示,取SA的中点G,连接FG、BG.
又∵F是SD的中点,∴FG∥AD,且FG=
AD,
∵E点是矩形ABCD的边BC的中点,∴BE∥AD,BE=
AD,
∴BE
GF,∴四边形BEFG是平行四边形,∴EF∥BG.
∵EF?平面SAB,BG?平面SBA.
∴EF∥平面SAB.
(2)∵平面SAB⊥平面ABCD,交线为AB,且AD⊥AB,
∴AD⊥平面SAB,
∴AD⊥BG,
由(1)可知:EF∥BG,
∴EF⊥AD.

又∵F是SD的中点,∴FG∥AD,且FG=
| 1 |
| 2 |
∵E点是矩形ABCD的边BC的中点,∴BE∥AD,BE=
| 1 |
| 2 |
∴BE
| ∥ |
| . |
∵EF?平面SAB,BG?平面SBA.
∴EF∥平面SAB.
(2)∵平面SAB⊥平面ABCD,交线为AB,且AD⊥AB,
∴AD⊥平面SAB,
∴AD⊥BG,
由(1)可知:EF∥BG,
∴EF⊥AD.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目