Question

1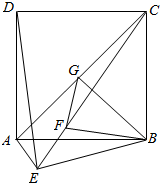．如图，直二面角D-AB-E中，四边形ABCD是边长为2的正方形，AE=EB=$\sqrt{2}$，F为CE上的点，且BF⊥CE，G为AC中点．
（Ⅰ）求证：AC⊥平面BGF；
（Ⅱ）求二面角B-AC-E的平面角正弦的大小；
（Ⅲ）求点D到平面ACE的距离．

Answer 1

分析 （1）证明CB⊥平面ABE．然后证明BF⊥AC．BG⊥AC．利用直线与平面垂直的判定定理证明AC⊥平面BGF．
（2）连结BD交AC于G，连结FG，说明∠BGF是二面角B-AC-E的平面角，通过求解直角△BFG，得到二面角B-AC-E的平面角正弦值．
（3）过点E作EO⊥AB交AB于点O，OE=1．利用V_D-ACE=V_E-ACD，求解点D到平面ACE的距离．

解答 （1）证明：∵二面角DABE为直二面角，且CB⊥AB，∴CB⊥平面ABE．
∴CB⊥AE．又∵AE=EB=$\sqrt{2}$，AB=2∴EB⊥AE．
∴AE⊥平面BCE．∴BF⊥AE．又∵BF⊥CE．
∴BF⊥平面ACE∴BF⊥AC．又∵BG⊥AC．
∴AC⊥平面BGF；  …（4分）
（2）解：连结BD交AC于G，连结FG，
∵正方形ABCD边长为2，∴BG⊥AC，BG=$\sqrt{2}$．∵BF⊥平面ACE，
由三垂线定理的逆定理得FG⊥AC，∴∠BGF是二面角B-AC-E的平面角．…（6分）
由（1）AE⊥平面BCE，又∵AE=EB，∴在等腰直角三角形AEB中，BE=$\sqrt{2}$．
又∵直角△BCE中，$\sqrt{{BC}^{2}+{BE}^{2}}=\sqrt{6}$，BF=$\frac{BC•BE}{EC}$=$\frac{2×\sqrt{2}}{\sqrt{6}}$=$\frac{2\sqrt{3}}{3}$，
∴直角△BFG中，sin∠BGF=$\frac{BF}{BG}$=$\frac{\frac{2\sqrt{3}}{3}}{\sqrt{2}}$=$\frac{\sqrt{6}}{3}$．
∴二面角B-AC-E的平面角正弦值为：$\frac{\sqrt{6}}{3}$；…（10分）
（3）解：过点E作EO⊥AB交AB于点O，OE=1．
∵二面角D-AB-E为直二面角，∴EO⊥平面ABCD．
设D到平面ACE的距离为h，
∵V_D-ACE=V_E-ACD，∴$\frac{1}{3}{S}_{△ACE}•h$=$\frac{1}{3}$S_△ACD•EO．…（12分）
∵AE⊥平面BCE，∴AE⊥EC．
∴h=$\frac{\frac{1}{2}AD•DC•EO}{\frac{1}{2}AE•EC}$=$\frac{\frac{1}{2}×2×2×1}{\frac{1}{2}×\sqrt{2}×\sqrt{6}}$=$\frac{2\sqrt{3}}{3}$．
∴点D到平面ACE的距离为$\frac{2\sqrt{3}}{3}$．…（14分）

点评 本题考查二面角的平面角的求法，找出二面角的平面角是求解角的关键，同时考查点、线、面之间距离，考查几何体的体积的求法，直线与平面垂直的判定定理的应用，考查空间想象能力以及计算能力．