题目内容
9.已知{xn}满足${x_n}=\sqrt{2+\root{3}{{3+\root{4}{{4+…+\root{n}{n}}}}},}(n≥2,n∈{N_+})$.(Ⅰ)设数列{ai}满足${a_i}=\root{i}{{i+\root{(i+1)}{{(i+1)+…+\root{(n+1)}{n+1}}}}},(i=2,3,4,…,n+1)$,设数列{bi}满足${b_i}=\root{i}{{i+\root{(i+1)}{{(i+1)+…+\root{n}{n}}}}},(i=2,3,4,…,n),{b_{n+1}}=0$.
求证:${a_i}^i-{b_i}^i={a_{i+1}}-{b_{i+1}}$(i=2,3,4,…,n);
(Ⅱ)求证:${x_n}<\sqrt{2}+1,(n≥2,n∈{N_+})$.
(参考公式:xn-yn=(x-y)•(xn-1+xn-2y+xn-3y2+…+yn-1),(n∈N+))
分析 (Ⅰ)利用条件,分类讨论,即可证明结论;
(Ⅱ)证明$\frac{{a}_{i+1}-{b}_{i+1}}{{a}_{i}-{b}_{i}}$>$i•i\frac{i-1}{i+1}$,由叠乘可得$\frac{{a}_{n+1}-{b}_{n+1}}{{a}_{2}-{b}_{2}}$>$(n!)•{n}^{\frac{n-1}{n+1}}$•…•${2}^{\frac{1}{3}}$,所以a2-b2<$\frac{(n+1)^{\frac{1}{n+1}}}{(n!)•{n}^{\frac{n-1}{n+1}}}$=$\frac{1}{n!}•(\frac{n+1}{{n}^{n-1}})^{\frac{1}{n+1}}$<$\frac{1}{n!}$(n≥3),其中n≥3时,$\frac{n+1}{{n}^{n-1}}$<$\frac{2n}{{n}^{2}}$<1显然成立.a2-b2=xn+1-xn,所以xn+1-xn<$\frac{1}{n!}$(n≥3),n=2时,x3-x2=$\sqrt{2+\root{3}{3}}$-$\sqrt{2}$<$\frac{1}{2!}$,可得xn+1-xn<$\frac{1}{n!}$(n≥2),由叠加法可得xn-x2<$\frac{1}{(n-1)!}$+…+$\frac{1}{2!}$(n≥3),再利用放缩,即可证明结论.
解答 证明:(Ⅰ)i=2,3,…,n-1时,aii-bii=$\root{i+1}{(i+1)+…\root{n+1}{n+1}}$-$\root{i+1}{(i+1)+…+\root{n}{n}}$=ai+1-bi+1,
i=n时,ann-bnn=an+1=an+1-bn+1,
所以${a_i}^i-{b_i}^i={a_{i+1}}-{b_{i+1}}$(i=2,3,4,…,n);
(Ⅱ)ai+1-bi+1=aii-bii=(ai-bi)(aii-1+aii-2bi+…+bii-1),
所以$\frac{{a}_{i+1}-{b}_{i+1}}{{a}_{i}-{b}_{i}}$=aii-1+aii-2bi+…+bii-1,
因为ai>bi>$\root{i}{i}$,
所以aii-1+aii-2bi+…+bii-1≥${i}^{\frac{i-1}{i}}$+${i}^{\frac{i-2}{i}}•{i}^{\frac{1}{i}}$+…+${i}^{\frac{i-1}{i}}$=$i•{i}^{\frac{i-1}{i}}$>$i•i\frac{i-1}{i+1}$,(i=2,3,…,n)
所以$\frac{{a}_{i+1}-{b}_{i+1}}{{a}_{i}-{b}_{i}}$>$i•i\frac{i-1}{i+1}$
由叠乘可得$\frac{{a}_{n+1}-{b}_{n+1}}{{a}_{2}-{b}_{2}}$>$(n!)•{n}^{\frac{n-1}{n+1}}$•…•${2}^{\frac{1}{3}}$
所以a2-b2<$\frac{(n+1)^{\frac{1}{n+1}}}{(n!)•{n}^{\frac{n-1}{n+1}}}$=$\frac{1}{n!}•(\frac{n+1}{{n}^{n-1}})^{\frac{1}{n+1}}$<$\frac{1}{n!}$(n≥3),其中n≥3时,$\frac{n+1}{{n}^{n-1}}$<$\frac{2n}{{n}^{2}}$<1显然成立.
a2-b2=xn+1-xn,所以xn+1-xn<$\frac{1}{n!}$(n≥3),n=2时,x3-x2=$\sqrt{2+\root{3}{3}}$-$\sqrt{2}$<$\frac{1}{2!}$,
所以xn+1-xn<$\frac{1}{n!}$(n≥2),
由叠加法可得xn-x2<$\frac{1}{(n-1)!}$+…+$\frac{1}{2!}$(n≥3),
因为x2=$\sqrt{2}$,
所以xn<$\sqrt{2}$+$\frac{1}{(n-1)!}$+…+$\frac{1}{2!}$(n≥3),
因为$\frac{1}{k!}$=$\frac{1}{k(k-1)…3•2•1}$≤$\frac{1}{{2}^{k-1}}$,
所以xn<$\sqrt{2}$+$\frac{1}{(n-1)!}$+…+$\frac{1}{2!}$≤$\sqrt{2}$+$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n-2}}$=$\sqrt{2}$+$\frac{\frac{1}{2}-\frac{1}{{2}^{n-1}}}{1-\frac{1}{2}}$<$\sqrt{2}$+1,
所以xn<$\sqrt{2}$+1(n≥3),
因为x2=$\sqrt{2}$<$\sqrt{2}$+1,
所以xn<$\sqrt{2}$+1(n≥2).
点评 本题考查不等式的证明,考查叠加法、叠乘法,考查学生分析解决问题的能力,有难度.

 阅读快车系列答案
阅读快车系列答案| A. | [-1,0] | B. | (-1,3] | C. | [0,1) | D. | {-1,3} |
| A. | c>b>a | B. | b>c>a | C. | a>c>b | D. | a>b>c |
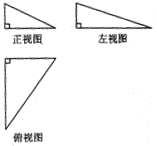 一个三棱锥的三视图如图所示,其正视图、左视图、俯视图的面积分别是1,2,4,则这个几何体的外接球的表面积为21π.
一个三棱锥的三视图如图所示,其正视图、左视图、俯视图的面积分别是1,2,4,则这个几何体的外接球的表面积为21π.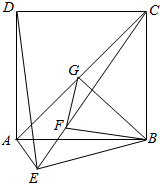 如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB=$\sqrt{2}$,F为CE上的点,且BF⊥CE,G为AC中点.
如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB=$\sqrt{2}$,F为CE上的点,且BF⊥CE,G为AC中点.