题目内容
16.若变量x,y满足$\left\{\begin{array}{l}2x-y+2≤0\\ x+2y-4≥0\\ x-3y+11≥0\end{array}\right.$,则z=2x+y的取值范围是[-1,6].分析 作出不等式组对应的平面区域,利用目标函数的几何意义,即可求z的取值范围.
解答 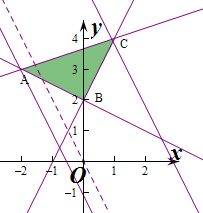 解:作出不等式组对应的平面区域如图:(阴影部分).
解:作出不等式组对应的平面区域如图:(阴影部分).
由z=2x+y得y=-2x+z,
平移直线y=-2x+z,
由图象可知当直线y=-2x+z经过点C时,直线y=-2x+z的截距最大,
此时z最大.
由$\left\{\begin{array}{l}{2x-y+2=0}\\{x-3y+11=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=1}\\{y=4}\end{array}\right.$,即C(1,4),
代入目标函数z=2x+y得z=2+4=6.
当直线y=-2x+z经过点A时,直线y=-2x+z的截距最小,
此时z最小.
由$\left\{\begin{array}{l}{x+2y-4=0}\\{x-3y+11=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-2}\\{y=3}\end{array}\right.$,即A(-2,3),
代入目标函数z=2x+y得z=-2×2+3=-1.
目标函数z=2x+y的取值范围是[-1,6],
故答案为:[-1,6].
点评 本题主要考查线性规划的应用,利用目标函数的几何意义,结合数形结合的数学思想是解决此类问题的基本方法.

练习册系列答案
相关题目
7.已知数列{an}满足a1=3,且an+1=an+log3(1+$\frac{1}{n}$),则a9=( )
| A. | 3 | B. | 4 | C. | log310+3 | D. | 5 |
11.已知集合A={x∈N|x-3≤0},B=f{x∈Z|x2+x-2≤0},则集合A∩B=( )
| A. | {1} | B. | {0,1} | C. | {0,1,2} | D. | {1,2} |
8. 如图一个倒三角形数表:
如图一个倒三角形数表:
它的排列规则是:第i(i=2,…,101)行的第j(j=1,2,…,102-i)个数ai.j=$\frac{{a}_{i-1,j}+{a}_{i-1,j+1}}{2}$,现设a1.j=xj-1(j=1,2,…,101),其中x>0,若a101.1=$\frac{1}{{2}^{50}}$,则x=( )
 如图一个倒三角形数表:
如图一个倒三角形数表:它的排列规则是:第i(i=2,…,101)行的第j(j=1,2,…,102-i)个数ai.j=$\frac{{a}_{i-1,j}+{a}_{i-1,j+1}}{2}$,现设a1.j=xj-1(j=1,2,…,101),其中x>0,若a101.1=$\frac{1}{{2}^{50}}$,则x=( )
| A. | $\sqrt{2}$-1 | B. | 1-$\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
5.执行如图程序框图其输出结果是( )


| A. | 29 | B. | 31 | C. | 33 | D. | 35 |
 为了调查高一新生中女生的体重情况,校卫生室随机选取20名女生作为样本测量她们的体重(单位:kg),获得的所有数据按照区间(40,45],(45,50],(50,55],(55,60]进行分组,得到频率分布直方图如图所示.已知样本中体重在区间(45,50]上的女生数与体重在区间(55,60]上的女生数之比为4:3.
为了调查高一新生中女生的体重情况,校卫生室随机选取20名女生作为样本测量她们的体重(单位:kg),获得的所有数据按照区间(40,45],(45,50],(50,55],(55,60]进行分组,得到频率分布直方图如图所示.已知样本中体重在区间(45,50]上的女生数与体重在区间(55,60]上的女生数之比为4:3.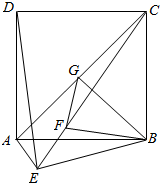 如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB=$\sqrt{2}$,F为CE上的点,且BF⊥CE,G为AC中点.
如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB=$\sqrt{2}$,F为CE上的点,且BF⊥CE,G为AC中点.