题目内容
10.已知数列{an}的前n项和为Sn=n2(Ⅰ)求通项公式an;
(Ⅱ) 令bn=a2n+3${\;}^{{a}_{n}}$求{bn的前n项和Tn.
分析 (Ⅰ)运用a1=S1=1,n>1时,an=Sn-Sn-1,计算即可得到通项公式an;
(Ⅱ) 运用数列求和方法:分组求和,分别运用等差数列和等比数列的求和公式的运用,即可得到所求和.
解答 解:(Ⅰ)数列{an}的前n项和为Sn=n2
则a1=S1=1,
an=Sn-Sn-1=n2-(n-1)2=2n-1,(n≥2),
综上可得an=2n-1;
(Ⅱ) bn=a2n+3${\;}^{{a}_{n}}$=4n-1+32n-1,
则前n项和Tn=$\frac{1}{2}$(3+4n-1)n+$\frac{3(1-{9}^{n})}{1-9}$
=(2n-1)n+$\frac{3}{8}$(9n-1).
点评 本题考查数列的通项和求和的关系,主要考查等差数列和等比数列的求和公式的运用,属于中档题.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
18.设a=0.36,b=log36,c=log510,则( )
| A. | c>b>a | B. | b>c>a | C. | a>c>b | D. | a>b>c |
5.执行如图程序框图其输出结果是( )


| A. | 29 | B. | 31 | C. | 33 | D. | 35 |
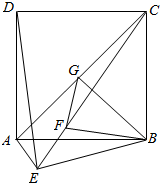 如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB=$\sqrt{2}$,F为CE上的点,且BF⊥CE,G为AC中点.
如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB=$\sqrt{2}$,F为CE上的点,且BF⊥CE,G为AC中点.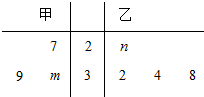 已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同,则二项式${(\frac{x}{m}+\frac{n}{x})^4}$展开式中的常数项为$\frac{128}{3}$.
已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同,则二项式${(\frac{x}{m}+\frac{n}{x})^4}$展开式中的常数项为$\frac{128}{3}$. 如图所示,在三棱锥P-ABC中,PD⊥平面ABC,且垂足D在棱AC上,AB=BC=$\sqrt{6}$,AD=1,CD=3,PD=$\sqrt{3}$.
如图所示,在三棱锥P-ABC中,PD⊥平面ABC,且垂足D在棱AC上,AB=BC=$\sqrt{6}$,AD=1,CD=3,PD=$\sqrt{3}$.