题目内容
6.如图空间四边形ABCD中,$\overrightarrow{AB}$⊥$\overrightarrow{BC}$,∠DAB=60°,$\overrightarrow{DA}$•$\overrightarrow{BC}$=-$\frac{1}{2}$,且|$\overrightarrow{DA}$|=|$\overrightarrow{AB}$|=|$\overrightarrow{BC}$|=1,则|$\overrightarrow{DC}$|=( )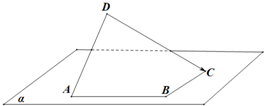
| A. | 2 | B. | 3 | C. | 1 | D. | $\sqrt{3}$ |
分析 通过向量的加法法则,利用向量的平方等于其模的平方计算即可.
解答 解:由题可知|$\overrightarrow{DC}$|=$\sqrt{|\overrightarrow{DC}{|}^{2}}$
=$\sqrt{[(\overrightarrow{DA}+\overrightarrow{AB})+\overrightarrow{BC}]^{2}}$
=$\sqrt{(\overrightarrow{DA}+\overrightarrow{AB})^{2}+2(\overrightarrow{DA}+\overrightarrow{AB})•\overrightarrow{BC}+{\overrightarrow{BC}}^{2}}$
=$\sqrt{{\overrightarrow{DA}}^{2}+2\overrightarrow{DA}•\overrightarrow{AB}+{\overrightarrow{AB}}^{2}+2\overrightarrow{DA}•\overrightarrow{BC}+2\overrightarrow{AB}•\overrightarrow{BC}+{\overrightarrow{BC}}^{2}}$
=$\sqrt{1-2×\frac{1}{2}+1-2×\frac{1}{2}+0+1}$
=1,
故选:C.
点评 本题考查平面向量数量积的运算,注意解题方法的积累,属于基础题.

练习册系列答案
相关题目
16.设复数z=-1-i(i为虚数单位),则$\frac{2-\overline{z}}{z}$对应的点位于( )
| A. | 第四象限 | B. | 第三象限 | C. | 第二象限 | D. | 第一象限 |
18.设a=0.36,b=log36,c=log510,则( )
| A. | c>b>a | B. | b>c>a | C. | a>c>b | D. | a>b>c |
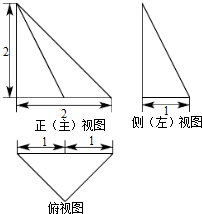
 一个三棱锥的三视图如图所示,其正视图、左视图、俯视图的面积分别是1,2,4,则这个几何体的外接球的表面积为21π.
一个三棱锥的三视图如图所示,其正视图、左视图、俯视图的面积分别是1,2,4,则这个几何体的外接球的表面积为21π.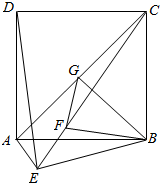 如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB=$\sqrt{2}$,F为CE上的点,且BF⊥CE,G为AC中点.
如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB=$\sqrt{2}$,F为CE上的点,且BF⊥CE,G为AC中点. A,B两名学生在5次英语口语测试中的成绩统计如茎叶图所示(十位作为茎).
A,B两名学生在5次英语口语测试中的成绩统计如茎叶图所示(十位作为茎).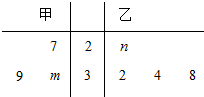 已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同,则二项式${(\frac{x}{m}+\frac{n}{x})^4}$展开式中的常数项为$\frac{128}{3}$.
已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同,则二项式${(\frac{x}{m}+\frac{n}{x})^4}$展开式中的常数项为$\frac{128}{3}$.