题目内容

17．若一个几何体的正视图和侧视图都是边长为2的正方形，俯视图是一个圆，则这个几何体的体积为（　　）
A．2πB．4πC．8πD．$\frac{8π}{3}$

分析 根据已知中几何体的正视图和侧视图都是边长为2的正方形，俯视图是一个圆，可得该几何体是一个底面半径为1，高为2的圆柱，代入圆柱体积公式，可得答案．

解答 解：∵几何体的正视图和侧视图都是边长为2的正方形，俯视图是一个圆，
∴该几何体是一个底面半径r=1，高h=2的圆柱，
故圆柱的体积V=πr2h=2π，
故选：A

点评 本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．

练习册系列答案
相关题目
7．设x∈R，记不超过x的最大整数为[x]，如[2.5]=2，[-2.5]=-3，令{x}=x-[x]，则{$\frac{\sqrt{5}+1}{2}$}，[$\frac{\sqrt{5}+1}{2}$]，$\frac{\sqrt{5}+1}{2}$，三个数构成的数列（　　）
A．是等比数列但不是等差数列B．是等差数列但不是等比数列
C．既是等差数列又是等比数列D．既不是等差数列也不是等比数列
8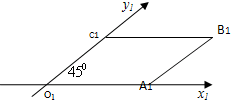．如图，一个正方形OABC在斜二测画法下的直观图是个一条边长为1的平行四边形，则正方形OABC的面积为（　　）
A．1B．4C．1或4D．不能确定
5．若函数f（x）唯一的一个零点同时在区间（0，8）、（0，6）、（0，4）、（0，2）内，那么下列命题中正确的是（　　）
A．函数f（x）在区间（0，1）内有零点B．函数f（x）在区间（0，1）或（1，2）内有零点
C．函数f（x）在区间[2，8）内无零点D．函数f（x）在区间（1，8）内无零点
12．在电脑游戏中，“主角”的生命机会往往被预先设定．如某枪战游戏，“主角”被设置生命6次，每次生命承受射击8次（即被击中8次就失去一次生命机会），假设射击为单发射击，如图是为“主角”耗用生命机会的过程设计的一个程序框图，请问判断框内应该填（　　）
A．i＜6B．i＜8C．i＞48D．i＜48
2．已知函数$f（x）=-\frac{3}{2}{x^2}+ax-1$；
（1）若函数f（x）在（-∞，+∞）上至少有一个零点，求a的取值范围；
（2）求函数f（x）在[1，2]上的最大值；
（3）若函数g（x）=f（x）+1在R上的最大值不大于$\frac{1}{6}$，又当$x∈[\frac{1}{4}，\frac{1}{2}]$时，$f（x）≥\frac{1}{8}$，求a得值．
9．已知两点M（1，0），N（-3，0）到直线l的距离分别为1和3，则满足条件的直线l的条数是3．
6．已知等腰三角形的一个底角的正弦值等于$\frac{5}{13}$，则这个等腰三角形的顶角的余弦值为（　　）
A．-$\frac{119}{169}$B．-$\frac{1}{3}$C．$\frac{1}{3}$D．$\frac{119}{169}$
7．设长方体的长、宽、高分别为1、2、1，其顶点都在一个球面上，则该球的表面积为（　　）
A．3πB．6πC．12πD．24π

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网