题目内容
2.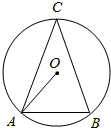 如图,⊙O是△ABC的外接圆,C是优弧AB上一点,设∠OAB=α,∠C=β.
如图,⊙O是△ABC的外接圆,C是优弧AB上一点,设∠OAB=α,∠C=β.(1)当α=36°时,求β的度数;
(2)猜想α与β之间的关系,并给予证明.
(3)若点C平分优弧AB,且BC2=3OA2,试求α的度数.
分析 (1)连接OB,根据三角形外心的性质可知:OA=OB;则在等腰△AOB中∠OBA=∠OAB;则再根据三角形内角和定理可以求得∠AOB的度数;最后根据圆周角定理可以求得β的度数;
(2)由(1)可猜想α与β之间的关系是α+β=90°;同(1)一样∠OBA=∠OAB=α,则∠AOB=180°-2α,β=∠C=$\frac{1}{2}$∠AOB,所以可求β=$\frac{1}{2}$(180°-2α)=90°-α,则α+β=90度;
(3)证明AC=BC=$\sqrt{3}$OA,过O作OK⊥AC于K,连接OC,由垂径定理可知:AK=$\frac{1}{2}$AC=$\frac{\sqrt{3}}{2}$OA,可得∠CAO=30°,∠ACB=2∠ACO=2∠CAO=60°,△ABC为正三角形,即可求α的度数.
解答  解:(1)连接OB,则OA=OB;∵∠OAB=36°,∴∠OBA=∠OAB=36°,
解:(1)连接OB,则OA=OB;∵∠OAB=36°,∴∠OBA=∠OAB=36°,
∵∠AOB=180°-∠OAB-∠OBA,∴∠AOB=180°-36°-36°=108°,
∴β=∠C=∠AOB=54°. …(3分)
(2)α与β之间的关系是α+β=90°;证明:∵∠OBA=∠OAB=α,∴∠AOB=180°-2α,
∵β=∠C=$\frac{1}{2}$∠AOB,∴β=$\frac{1}{2}$(180°-2α)=90°-α,∴α+β=90°.…(6分)
(3)∵点C平分优弧AB,
∴$\widehat{AC}=\widehat{BC}$
∴AC=BC,
又∵BC2=3OA2,∴AC=BC=$\sqrt{3}$OA,
过O作OK⊥AC于K,连接OC,由垂径定理可知:AK=$\frac{1}{2}$AC=$\frac{\sqrt{3}}{2}$OA,∴∠CAO=30°
易得:∠ACB=2∠ACO=2∠CAO=60°,∴△ABC为正三角形,
则:α=∠CAB-∠CAO=30° …(10分)
点评 本题考查了三角形的外接圆的性质以及圆周角定理.要熟练掌握这些性质定理才能灵活运用.

 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案| A. | [-1,2] | B. | [-2,2] | C. | [-2,-1] | D. | [-1,1] |
命题①:对任意有限集A,B,“A≠B”是“|A-B|>0”的充要条件;
命题②:对任意有限集A,B,C,有|A-C|≤|A-B|+|B-C|.( )
| A. | 命题①和命题②都成立 | B. | 命题①和命题②都不成立 | ||
| C. | 命题①成立,命题②不成立 | D. | 命题①不成立,命题②成立 |
| A. | 5 | B. | 8 | C. | $\sqrt{10}$ | D. | 64 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |