题目内容
13.双曲线${y^2}-\frac{x^2}{2}=1$的焦距是2$\sqrt{3}$,渐近线方程是$y=±\frac{\sqrt{2}}{2}x$.分析 利用双曲线方程,求出双曲线的几何量,然后求解即可.
解答 解:双曲线${y^2}-\frac{x^2}{2}=1$可得a=1,b=$\sqrt{2}$,双曲线的焦距是2c=2$\sqrt{1+2}$=2$\sqrt{3}$.
双曲线的渐近线方程为:$y=±\frac{\sqrt{2}}{2}x$.
故答案为:$2\sqrt{3},y=±\frac{{\sqrt{2}}}{2}x$.
点评 本题考查双曲线的简单性质,考查计算能力.

练习册系列答案
相关题目
1.设向量$\{\overrightarrow a,\overrightarrow b,\overrightarrow c\}$是空间一个基底,则一定可以与向量$\overrightarrow p=\overrightarrow a+\overrightarrow b,\overrightarrow q=\overrightarrow a-\overrightarrow b$构成空间的另一个基底的向量是( )
| A. | $\overrightarrow a$ | B. | $\overrightarrow b$ | C. | $\overrightarrow c$ | D. | $\overrightarrow{a}$或$\overrightarrow{b}$ |
8.已知实数a,b满足不等式log2a<log3b,则不可能成立的是( )
| A. | 0<b<a<1 | B. | 0<a<b<1 | C. | 1<a<b | D. | 1<b<a |
18.在三棱锥S-ABC中,SA⊥平面ABC,SA=4,底面△ABC是边长为3的正三角形,则三棱锥S-ABC的外接球的表面积为( )
| A. | 19π | B. | 28π | C. | 43π | D. | 76π |
5.函数$f(x)={log_2}(a-{2^x})+x-2$,当$x∈[0,\frac{1}{2}]$时,f(x)≤0恒成立,则实数a的取值范围是( )
| A. | (-∞,4] | B. | $(\sqrt{2},4]$ | C. | $(-∞,3\sqrt{2}]$ | D. | $(\sqrt{2},3\sqrt{2}]$ |
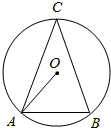 如图,⊙O是△ABC的外接圆,C是优弧AB上一点,设∠OAB=α,∠C=β.
如图,⊙O是△ABC的外接圆,C是优弧AB上一点,设∠OAB=α,∠C=β.