题目内容
11.已知$\overrightarrow{a}=(1,x)$和$\overrightarrow{b}=(x+2,-2)$,若$\overrightarrow{a}⊥\overrightarrow{b}$,则|$\overrightarrow{a}+\overrightarrow{b}$|=( )| A. | 5 | B. | 8 | C. | $\sqrt{10}$ | D. | 64 |
分析 由题意可得x+2-2x=0,解方程可得x,即可求出|$\overrightarrow{a}+\overrightarrow{b}$|.
解答 解:∵$\overrightarrow{a}=(1,x)$和$\overrightarrow{b}=(x+2,-2)$,$\overrightarrow{a}⊥\overrightarrow{b}$,
∴x+2-2x=0,
解得x=2,
∴|$\overrightarrow{a}+\overrightarrow{b}$|=|(5,0)|=5.
故选:A.
点评 本题考查数量积与向量的垂直关系,属基础题.

练习册系列答案
相关题目
1.设向量$\{\overrightarrow a,\overrightarrow b,\overrightarrow c\}$是空间一个基底,则一定可以与向量$\overrightarrow p=\overrightarrow a+\overrightarrow b,\overrightarrow q=\overrightarrow a-\overrightarrow b$构成空间的另一个基底的向量是( )
| A. | $\overrightarrow a$ | B. | $\overrightarrow b$ | C. | $\overrightarrow c$ | D. | $\overrightarrow{a}$或$\overrightarrow{b}$ |
19.下列说法正确的是( )
| A. | -1∈N | B. | $\sqrt{2}$∈Q | C. | π∉R | D. | ∅⊆Z |
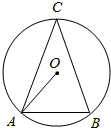 如图,⊙O是△ABC的外接圆,C是优弧AB上一点,设∠OAB=α,∠C=β.
如图,⊙O是△ABC的外接圆,C是优弧AB上一点,设∠OAB=α,∠C=β.