已知$\frac{1+tanα}{1-tanα}=\frac{4}{3}$.则$tan$=$\frac{4}{3}$.tanα=$\frac{1}{7}$．题目和参考答案——青夏教育精英家教网——

题目内容

14．已知$\frac{1+tanα}{1-tanα}=\frac{4}{3}$，则$tan（α+\frac{π}{4}）$=$\frac{4}{3}$，tanα=$\frac{1}{7}$．

分析由条件利用两角和的正切公式，求得$tan（α+\frac{π}{4}）$以及tanα的值．

解答解：∵$\frac{1+tanα}{1-tanα}=\frac{4}{3}$=$tan（α+\frac{π}{4}）$，∴$tan（α+\frac{π}{4}）$=$\frac{4}{3}$．
再根据$\frac{1+tanα}{1-tanα}=\frac{4}{3}$，求得tanα=$\frac{1}{7}$，
故答案为：$\frac{4}{3}$； $\frac{1}{7}$．

点评本题主要考查两角和的正切公式的应用，属于基础题．

练习册系列答案

课课练习系列答案

云南师大附小一线名师核心试卷系列答案

夺冠计划课时测控系列答案

课时精练系列答案

课时全练讲练测全程达标系列答案

课时天天练系列答案

课时学案系列答案

课堂达标100分系列答案

课堂过关循环练系列答案

课堂检测10分钟系列答案

相关题目

4．根据对数函数的图象和性质填空．
（1）已知函数y=log₂x，则当x＞0时，y∈（-∞，+∞），当x＞1时，y∈（0，+∞）．当0＜x＜1时，y∈（-∞，0）；当x＞4时，y∈（2，+∞）．
（2）已知函数y=log${\;}_{\frac{1}{3}}$x，则当0＜x＜1时，y∈（0，+∞），当x＞1时，y∈（-∞，0）．当x＞5时，y∈（-∞，log${\;}_{\frac{1}{3}}$5）；当0＜x＜2时，y∈（log${\;}_{\frac{1}{3}}$2，+∞）；当y＞2时，x∈（0，$\frac{1}{9}$）．

5．函数$f（x）={log_2}（a-{2^x}）+x-2$，当$x∈[0，\frac{1}{2}]$时，f（x）≤0恒成立，则实数a的取值范围是（　　）

$（\sqrt{2}，4]$

$（-∞，3\sqrt{2}]$

$（\sqrt{2}，3\sqrt{2}]$

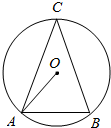如图，⊙O是△ABC的外接圆，C是优弧AB上一点，设∠OAB=α，∠C=β．
（1）当α=36°时，求β的度数；
（2）猜想α与β之间的关系，并给予证明．
（3）若点C平分优弧AB，且BC²=3OA²，试求α的度数．

9．若0＜3^a=4^b＜1，则a，b的大小关系是a＜b．

19．下列说法正确的是（　　）

6．已知函数f（x）的定义域为（0，4），函数g（x）=$\frac{{f（{x+1}）}}{{\sqrt{x-1}}}$的定义域为集合A，集合B={x|a＜x＜2a-1}，若A∩B=B，求实数a的取值范围．

3．已知函数f（x）=x²-ax，（a＞0），$g（x）=sinxsin（{x+\frac{π}{6}}）-\frac{{\sqrt{3}}}{4}$，命题p：a_n=f（n）是递增数列，命题q：g（x）在（a，π）上有且仅有2条对称轴．
①求g（x）的周期和单调递增区间；
②若p∧q为真，求a的取值范围．

4．已知各顶点都在同一个球面上的正四棱锥高为3，底面边长为$\sqrt{6}$，则这个球的表面积是16π．