题目内容
10．已知数列{an}的前n项和为Sn，且Sn+an=4，n∈N*（Ⅰ）求数列{an}的通项公式；
（Ⅱ）已知bn=2n-17（n∈N*），记cn=log2an-bn．求数列{cn}的前n项和Tn的最大值．
分析 （Ⅰ）通过递推关系式直接求出a1，利用Sn+an=4，Sn-1+an-1=4，两式相减得，2an=an-1，说明数列{an}是以2为首项，公比为$\frac{1}{2}$的等比数列，求出通项公式．
（Ⅱ）化简cn=log2an-bn=19-3n，判断数列{cn}是等差数列，且公差d＜0，{cn}的前n项和Tn最大值是它的所有正项数之和，求解即可．
解答 解：（Ⅰ）a1+a1=4，所以a1=2…（1分）
由Sn+an=4得n≥2时，Sn-1+an-1=4…（2分）
两式相减得，2an=an-1，$\frac{a_n}{{{a_{n-1}}}}=\frac{1}{2}$，…（3分）
数列{an}是以2为首项，公比为$\frac{1}{2}$的等比数列，
所以${a_n}={2^{2-n}}$（n∈N*）…（5分）
（Ⅱ）由题，cn=log2an-bn=19-3n…（6分）
在{cn}中，cn-cn-1=-3，所以数列{cn}是等差数列，且公差d＜0…（7分）
所以{cn}的前n项和Tn最大值是它的所有正项数之和．…（9分）
${c_n}≥0，即19-3n≥0，得n≤\frac{19}{3}$…（10分）
所以n=6时取得最大值．…（11分）
即（Sn）max=S6=51…（12分）
点评 本题考查递推关系式的应用，数列求和以及等差数列等比数列的判断，考查计算能力．
练习册系列答案
小学教材完全解读系列答案
相关题目
17．若sinxcosy+cosxsiny=$\frac{1}{2}$，cos2x-cos2y=$\frac{2}{3}$，则sin（x-y）等于（ ）
| A． | $\frac{1}{3}$ | B． | -$\frac{1}{3}$ | C． | $\frac{2}{3}$ | D． | -$\frac{2}{3}$ |
5．
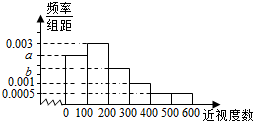某普通高中为了了解学生的视力状况，随机抽查了100名高二年级学生和100名高三年级学生，对这些学生配戴眼镜的度数（简称：近视度数）进行统计，得到高二学生的频数分布表和高三学生频率分布直方图如下：
将近视程度由低到高分为4个等级：当近视度数在0-100时，称为不近视，记作0；当近视度数在100-200时，称为轻度近视，记作1；当近视度数在200-400时，称为中度近视，记作2；当近视度数在400以上时，称为高度近视，记作3．
（Ⅰ）从该校任选1名高二学生，估计该生近视程度未达到中度及以上的概率；
（Ⅱ）设a=0.0024，从该校任选1名高三学生，估计该生近视程度达到中度或中度以上的概率；
（Ⅲ）把频率近似地看成概率，用随机变量X，Y分别表示高二、高三年级学生的近视程度，若EX=EY，求b．
某普通高中为了了解学生的视力状况，随机抽查了100名高二年级学生和100名高三年级学生，对这些学生配戴眼镜的度数（简称：近视度数）进行统计，得到高二学生的频数分布表和高三学生频率分布直方图如下：| 近视度数 | 0-100 | 100-200 | 200-300 | 300-400 | 400以上 |
| 学生频数 | 30 | 40 | 20 | 10 | 0 |
（Ⅰ）从该校任选1名高二学生，估计该生近视程度未达到中度及以上的概率；
（Ⅱ）设a=0.0024，从该校任选1名高三学生，估计该生近视程度达到中度或中度以上的概率；
（Ⅲ）把频率近似地看成概率，用随机变量X，Y分别表示高二、高三年级学生的近视程度，若EX=EY，求b．