题目内容
14.一条铁路原有n个车站,为了适应客运需要,新增加了m(m>1)个车站,客运车票增加了62种,问原有多少个车站?现有多少个车站?分析 由排列知识,可得${A}_{n+m}^{2}$-${A}_{n}^{2}$=62,从而得出n=$\frac{31}{m}$-$\frac{1}{2}$(m-1),1<m<$\frac{1+\sqrt{249}}{2}$,1<m≤8,验证即可得出结论.
解答 解:∵原有车站n个,
∴原有客运车票${A}_{n}^{2}$种,
又现有(n+m)个车站,现有客运车票${A}_{n+m}^{2}$种,
∴${A}_{n+m}^{2}$-${A}_{n}^{2}$=62,
∴(n+m)(n+m-1)-n(n-1)=62,
∴n=$\frac{31}{m}$-$\frac{1}{2}$(m-1)>0,
∴m2-m-62<0,
又m>1,从而得出1<m<$\frac{1+\sqrt{249}}{2}$,
∴1<m≤8,
即m=2时,n=$\frac{31}{2}-\frac{2-1}{2}$=15,
当m=3、4、5、6、7、8时,n均不为整数,
故只有n=15,m=2,
即原有15个车站,现有17个车站.
点评 本题考查排列知识的运用,考查学生的计算能力,确定n=$\frac{31}{m}$-$\frac{1}{2}$(m-1),1<m<$\frac{1+\sqrt{249}}{2}$是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.设C表示复数集,A={x∈C|x2+1=0},则集合A的子集个数是( )
| A. | 0 | B. | 1 | C. | 3 | D. | 4 |
8.某程序框图如图所示,运行相应该程序,那么输出的k的值是( )
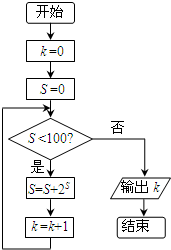

| A. | 4 | B. | 5 | C. | 6 | D. | 7 |