题目内容
【题目】已知曲线y=x3+x-2在点P0处的切线l1平行于直线4x-y-1=0,且点P0在第三象限.
(1)求P0的坐标;(2)若直线l⊥l1,且l也过切点P0,求直线l的方程.
【答案】(1)(-1,-4);(2)x+4y+17=0.
【解析】试题分析:(1)根据曲线方程求出导函数,因为已知直线4x-y-1=0的斜率为4,根据切线与已知直线平行得到斜率相等都为4,所以令导函数等于4得到关于x的方程,求出方程的解,即为切点P0的横坐标,代入曲线方程即可求出切点的纵坐标,又因为切点在第3象限,进而写出满足题意的切点的坐标;
(2)由直线l1的斜率为4,根据两直线垂直时斜率的乘积为-1,得到直线l的斜率为![]() ,又根据(1)中求得的切点坐标,写出直线l的方程即可.
,又根据(1)中求得的切点坐标,写出直线l的方程即可.
试题解析:
(1)证明:由y=x3+x-2,得y′=3x2+1.
由已知令3x2+1=4,解之得x=±1.
当x=1时,y=0;当x=-1时,y=-4.
又∵点P0在第三象限,∴切点P0的坐标为(-1,-4).
(2)∵直线l⊥l1,l1的斜率为4,∴直线l的斜率![]() .
.
∵l过切点P0,点P0的坐标为(-1,-4),
∴直线l的方程为y+4=-![]() (x+1),即x+4y+17=0.
(x+1),即x+4y+17=0.

 名校课堂系列答案
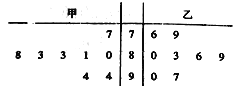
名校课堂系列答案【题目】(本小题满分12分)某企业生产的一批产品中有一、二、三等品及次品共四个等级,1件不同等级产品的利润(单位:元)如表1,从这批产品中随机抽取出1件产品,该件产品为不同等级的概率如表2.
等级 | 一等品 | 二等品 | 三等品 | 次品 |
|
| |
|
|
等级 | 一等品 | 二等品 | 三等品 | 次品 |
利润 | |
|
|
|
表1 表2
若从这批产品中随机抽取出的1件产品的平均利润(即数学期望)为![]() 元.
元.
(1) 设随机抽取1件产品的利润为随机变量![]() ,写出
,写出![]() 的分布列并求出
的分布列并求出![]() 的值;
的值;
(2) 从这批产品中随机取出3件产品,求这3件产品的总利润不低于17元的概率.