题目内容
【题目】已知函数f(x)=x2﹣4x+a+3,g(x)=mx+5﹣2m
(1)当a=﹣3,m=0时,求方程f(x)﹣g(x)=0的解;
(2)若方程f(x)=0在[﹣1,1]上有实数根,求实数a的取值范围;
(3)当a=0时,若对任意的x1∈[1,4],总存在x2∈[1,4],使f(x1)=g(x2)成立,求实数m的取值范围.
【答案】
(1)解:当a=﹣3,m=0时,求方程f(x)﹣g(x)=0化为x2﹣4x﹣5=0,
解得:x=﹣1或x=5
(2)解:∵函数f(x)=x2﹣4x+a+3的对称轴是x=2,
∴f(x)在区间[﹣1,1]上是减函数,
∵函数在区间[﹣1,1]上存在零点,则必有:
![]() ,即
,即 ![]() ,解得﹣8≤a≤0.
,解得﹣8≤a≤0.
故所求实数a的取值范围为[﹣8,0]
(3)解:若对任意的x1∈[1,4],总存在x2∈[1,4],使f(x1)=g(x2)成立,
只需函数y=f(x)的值域为函数y=g(x)的值域的子集.
f(x)=x2﹣4x+3,x∈[1,4]的值域为[﹣1,3],
下面求g(x)=mx+5﹣2m的值域.
①当m=0时,g(x)=5﹣2m为常数,不符合题意舍去;
②当m>0时,g(x)的值域为[5﹣m,5+2m],要使[﹣1,3][5﹣m,5+2m],
需 ![]() ,解得m≥6;
,解得m≥6;
③当m<0时,g(x)的值域为[5+2m,5﹣m],要使[﹣1,3][5+2m,5﹣m],
需 ![]() ,解得m≤﹣3.
,解得m≤﹣3.
综上,m的取值范围为(﹣∞,﹣3]∪[6,+∞)
【解析】(1)直接把a=﹣3,m=0代入方程,求解一元二次方程得答案;(2)求出函数f(x)的对称轴,得到f(x)在区间[﹣1,1]上是减函数,由函数在区间[﹣1,1]上存在零点得不等式组 ![]() ,求解不等式组得实数a的取值范围;(3)把对任意的x1∈[1,4],总存在x2∈[1,4],使f(x1)=g(x2)成立转化为函数y=f(x)的值域为函数y=g(x)的值域的子集,然后求g(x)的值域得答案.
,求解不等式组得实数a的取值范围;(3)把对任意的x1∈[1,4],总存在x2∈[1,4],使f(x1)=g(x2)成立转化为函数y=f(x)的值域为函数y=g(x)的值域的子集,然后求g(x)的值域得答案.
【考点精析】根据题目的已知条件,利用函数的零点的相关知识可以得到问题的答案,需要掌握函数的零点就是方程的实数根,亦即函数的图象与轴交点的横坐标.即:方程有实数根,函数的图象与坐标轴有交点,函数有零点.

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案【题目】某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在下图中的两条线段上,该股票在30天内(包括30天)的日交易量Q(万股)与时间t(天)的部分数据如下表所示. 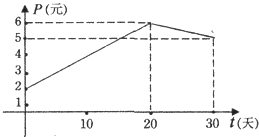
第t天 | 4 | 10 | 16 | 22 |
Q(万股) | 36 | 30 | 24 | 18 |
(1)根据提供的图象,写出该种股票每股交易价格P(元)与时间t(天)所满足的函数关系式;
(2)根据表中数据确定日交易量Q(万股)与时间t(天)的一次函数关系式;
(3)在(2)的结论下,用y(万元)表示该股票日交易额,写出y关于t的函数关系式,并求出这30天中第几日交易额最大,最大值为多少?