题目内容
【题目】已知双曲线x2﹣ 
=1，过点P（2，1）能否作一条直线l，与双曲线交于A，B两点，且点P是线段AB的中点？
【答案】解：设点A（x1 ， y1），点B（x2 ， y2），P（x0 ， y0），则2x12﹣y12=2 ①
2x22﹣y22=2 ②
①﹣②得
2（x1+x2）（x1﹣x2）﹣（y1+y2）（y1﹣y2）=0，
2×2x0﹣2y0
=0，
∴8﹣2k=0，
∴k=4，
∴y﹣1=4（x﹣2），
∴直线l的方程为4x﹣y﹣7=0，
故答案为：4x﹣y﹣7=0
【解析】首先，设点A（x1 ， y1），点B（x2 ， y2），P（x0 ， y0），得到2x12﹣y12=2 ①，2x22﹣y22=2 ②然后，①﹣②并结合有关中点坐标公式求解．
练习册系列答案
阳光课堂课时优化作业系列答案
相关题目
【题目】某上市股票在30天内每股的交易价格P（元）与时间t（天）组成有序数对（t，P），点（t，P）落在下图中的两条线段上，该股票在30天内（包括30天）的日交易量Q（万股）与时间t（天）的部分数据如下表所示．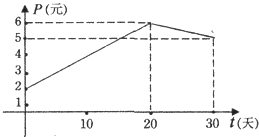 
第t天 | 4 | 10 | 16 | 22 |
Q（万股） | 36 | 30 | 24 | 18 |
（1）根据提供的图象，写出该种股票每股交易价格P（元）与时间t（天）所满足的函数关系式；
（2）根据表中数据确定日交易量Q（万股）与时间t（天）的一次函数关系式；
（3）在（2）的结论下，用y（万元）表示该股票日交易额，写出y关于t的函数关系式，并求出这30天中第几日交易额最大，最大值为多少？
