题目内容
【题目】已知函数![]() 。
。
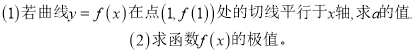
【答案】(1) ![]() (2)
(2) 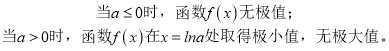
【解析】试题分析:
(1)首先求得函数的导函数,然后结合切线与导数的关系得到关于实数a的方程,解方程可得a=e;
(2)结合导函数的解析式与函数极值的关系分类讨论可得:当a≤0时,函数f(x)无极值,当a>0时,函数f(x)在x=lna处取得极小值,无极大值.
试题解析:
由f(x)=x-1+![]() 且其定义域为R
且其定义域为R
(1)曲线y=f(x)在(1,f(1))处切线平行于x轴,则f' (1)=0即![]()
(2)由f' (x)=1-![]() 且其定义域为R
且其定义域为R
①.当a≤0时f' (x)>0在R上恒成立,f(x)在(-∞,+∞)上单调递增,故f(x)无极值
②当a>0时,f' (x)= ![]() 由f' (x)>0得x>lna,由f' (x)<0得x<lna,
由f' (x)>0得x>lna,由f' (x)<0得x<lna,
即f(x)在(-∞,lna)单调递减,(lna,+∞)单调递增.
故f(x)在(-∞,+∞)上x=lna处取得极小值,f(lna)=lna无极大值.
综上所述:当a≤0时,函数f(x)无极值,当a>0时,函数f(x)在x=lna处取得极小值,无极大值.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目