��Ŀ����
ij��������һ�ֲ�Ʒ��ԭ���Ϸ�Ϊÿ��40Ԫ������x��ʾ�ó��������ֲ�Ʒ���ܼ��������������������ȷ���Ϊÿ��0��05xԪ���ָó�ְ�����ʹ̶�֧��12500Ԫ��
��1����ÿ����Ʒ�ijɱ���P��x����Ԫ����ʾ�ɲ�Ʒ����x�ĺ���������ÿ����Ʒ����ͳɱ��ѣ�
��2������ó����������ֲ�Ʒ������x������3000�����Ҳ�Ʒ��ȫ�����ۣ������г����飺ÿ����Ʒ�����ۼ�Q��x�����Ʒ����x�����¹�ϵ��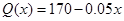 �������������ټ���Ʒ����������ߣ���������=�����۶�-�ܵijɱ���
�������������ټ���Ʒ����������ߣ���������=�����۶�-�ܵijɱ���
��1��90
��2������650����Ʒʱ����������ߣ����������Ϊ29750Ԫ
��������������⣺����
�ɻ�������ʽ��
���ҽ��� ����
���� ʱ���Ⱥų���
ʱ���Ⱥų���
�� ���ɱ�����СֵΪ
���ɱ�����СֵΪ Ԫ��
Ԫ��
������������Ϊ Ԫ����
Ԫ����

�� ʱ,
ʱ,
������650����Ʒʱ����������ߣ����������Ϊ29750Ԫ��
���㣺����ģ�͵�����
��������Ҫ�ǿ����˺���ģ�����ã���Ͼ�ֵ����ʽ�������ֵ�������е��⡣

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�2013�꣬������������59����������������һ���¡��������ͳ�ƣ������д�1��1����1��30����30������26�����������������������������ָ����AQI�������涨�����У�������������ָ����Ϊ���������У��ж���Ⱦ���ļ�����ָ��Ϊ151��200���ض���Ⱦ���弶����ָ��Ϊ201��300��������Ⱦ����������ָ������300�� �����1�Ǹù۲���¼��4���AQIָ�� �뵱��Ŀ���ˮƽ�ɼ���
�뵱��Ŀ���ˮƽ�ɼ��� ��ǧ�ף����������2��ij����۲���¼�ı���1��1�յ�1��30��AQIָ��Ƶ��ͳ�ƽ����
��ǧ�ף����������2��ij����۲���¼�ı���1��1�յ�1��30��AQIָ��Ƶ��ͳ�ƽ����
��1��AQIָ�� �뵱��Ŀ���ˮƽ�ɼ���
�뵱��Ŀ���ˮƽ�ɼ��� ��ǧ�ף����
��ǧ�ף����
AQIָ�� |  |  |  |  |
�����ɼ��� ��ǧ�ף� ��ǧ�ף� |  |  |  |  |
| AQIָ�� |  |  |  |  |  |
| Ƶ�� | 3 | 6 | 12 | 6 | 3 |
 �����ݱ�1�����ݣ����
�����ݱ�1�����ݣ���� ����
���� �����Իع鷽�̣�
�����Իع鷽�̣������ݱ�2������30��AQIָ����ƽ��ֵ.
������С���˷������Իع鷽��ϵ����ʽ
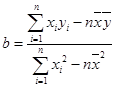 ��
�� ��
�� ��һ��������Ҫ�����������������ڳ��м��������������ڳ����ң���֪�ӳ��м�������ֻ��������·����ͨ����������·���õ�ʱ�以��Ӱ�죮
�ݵ���ͳ�ƣ�ͨ����������·�ӳ��м������ҵ�200����������ʱ���Ƶ���ֲ����±���
| ���õ�ʱ�䣨������ | 10 | 11 | 12 | 13 |
| ͨ����·1��Ƶ�� | 20 | 40 | 20 | 20 |
| ͨ����·2��Ƶ�� | 10 | 40 | 40 | 10 |
(��)Ϊ�˾��������ڸ���������ʱ���ڽ��������������ң���������A������BӦ���ѡ����Ե�·����
(��)��ͨ����·1����·2�ġ�һ���Է��á��ֱ�Ϊ
 ��Ԫ��
��Ԫ�� ��Ԫ(�������ú��Բ���)����������������̳е������������ǡ����Լ�����ڵ��콫�����͵�����������һ����֧����������40��Ԫ������Լ������ǰ�͵���ÿ��ǰһ�������̽���֧����������2��Ԫ������Լ�����ں��͵���ÿ�ٵ�һ�죬�����̽���֧����������2��Ԫ���������A��B���ڰ�(��)��ѡ·���������ԱȽ���������Ϊ�����̻�õ�ë�������(ע��ë����=(������֧���������̵ķ���)һ(һ���Է���)) ��
��Ԫ(�������ú��Բ���)����������������̳е������������ǡ����Լ�����ڵ��콫�����͵�����������һ����֧����������40��Ԫ������Լ������ǰ�͵���ÿ��ǰһ�������̽���֧����������2��Ԫ������Լ�����ں��͵���ÿ�ٵ�һ�죬�����̽���֧����������2��Ԫ���������A��B���ڰ�(��)��ѡ·���������ԱȽ���������Ϊ�����̻�õ�ë�������(ע��ë����=(������֧���������̵ķ���)һ(һ���Է���)) �� 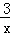 ��Ԫ��
��Ԫ�� ��Ԫ��
��Ԫ�� ���溯����
���溯���� ��ż������
��ż������ ��ֵ��
��ֵ�� ��
�� ������
������ ���������ʵ��
���������ʵ�� ��ȡֵ��Χ��
��ȡֵ��Χ��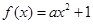 ��
�� ����
���� ��
�� ��
�� �����й������ߣ���
�����й������ߣ��� ��ֵ��
��ֵ�� ʱ������
ʱ������ ������
������ �ϵ����ֵ��
�ϵ����ֵ�� ǧ���ٶ�������ʻ130ǧ��
ǧ���ٶ�������ʻ130ǧ��
 ����λ��ǧ��/Сʱ�����������͵ļ۸���ÿ��6Ԫ��������ÿСʱ����
����λ��ǧ��/Сʱ�����������͵ļ۸���ÿ��6Ԫ��������ÿСʱ���� ����˾���Ĺ�����ÿСʱ30Ԫ��
����˾���Ĺ�����ÿСʱ30Ԫ�� ����
����