题目内容
某造船公司年造船量是20艘,已知造船x艘的产值函数为R(x)=3700x+45x2-10x3(单位:万元),成本函数为C(x)=460x+5000(单位:万元),又在经济学中,函数f(x)的边际函数Mf(x)定义为Mf(x)=f(x+1)-f(x).
(1)求利润函数P(x)及边际利润函数MP(x);(提示:利润=产值-成本)
(2)问年造船量安排多少艘时,可使公司造船的年利润最大?
(1)P(x)= -10x3+45x2+3 240x-5 000(x∈N*,且1≤x≤20);
MP(x)=P(x+1)-P(x)=-30x2+60x+3 275 (x∈N*,且1≤x≤19)
(2)x=12时,P(x)有最大值
解析试题分析:解:(1)P(x)=R(x)-C(x)=-10x3+45x2+3 240x-5 000(x∈N*,且1≤x≤20);
MP(x)=P(x+1)-P(x)=-30x2+60x+3 275 (x∈N*,且1≤x≤19). 4分
(2)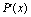 =-30x2+90x+3 240=-30(x-12)(x+9),
=-30x2+90x+3 240=-30(x-12)(x+9),
∵x>0,∴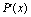 =0时,x=12, 8分
=0时,x=12, 8分
∴当0<x<12时,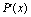 >0,当x>12时,
>0,当x>12时,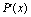 <0,
<0,
∴x=12时,P(x)有最大值. 11分
即年造船量安排12艘时,可使公司造船的年利润最大. 12分
考点:函数的运用
点评:主要是考查了函数模型的运用,分析问题和解决问题能力的运用,属于中档题。

练习册系列答案
相关题目

 .
.  时取得极值?说明理由;
时取得极值?说明理由; ,4]时,函数f(x)与g(x)的图像有两个公共点,求c的取值范围.
,4]时,函数f(x)与g(x)的图像有两个公共点,求c的取值范围. 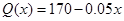 ,试问生产多少件产品,总利润最高?(总利润=总销售额-总的成本)
,试问生产多少件产品,总利润最高?(总利润=总销售额-总的成本)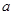 米的一块正方形铁皮的四角各截去一个大小相同的小正方形,然后将四边折起做成一个无盖的方盒.欲使所得的方盒有最大容积,截去的小正方形的边长应为多少米?方盒的最大容积为多少?
米的一块正方形铁皮的四角各截去一个大小相同的小正方形,然后将四边折起做成一个无盖的方盒.欲使所得的方盒有最大容积,截去的小正方形的边长应为多少米?方盒的最大容积为多少?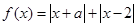
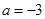 时,求不等式
时,求不等式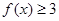 的解集; (2)若
的解集; (2)若 的解集包含
的解集包含 ,求
,求 的取值范围.
的取值范围. 是偶函数,
是偶函数, ,
, 的值;(2)当
的值;(2)当 时,求
时,求 的解集;
的解集; 的图象总在
的图象总在 的图象上方,求实数
的图象上方,求实数 的取值范围.
的取值范围. ,
, 是定义域为R上的奇函数.
是定义域为R上的奇函数. 的值,并证明当
的值,并证明当 时,函数
时,函数 ,函数
,函数 ,
, ,求
,求 的值域;
的值域;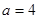 ,试问是否存在正整数
,试问是否存在正整数 ,使得
,使得 对
对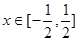 恒成立?若存在,请求出所有的正整数
恒成立?若存在,请求出所有的正整数