题目内容
已知函数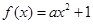 (
( ),
), .
.
(Ⅰ)若曲线 与
与 在它们的交点
在它们的交点 处具有公共切线,求
处具有公共切线,求 的值;
的值;
(Ⅱ)当 时,求函数
时,求函数 在区间
在区间 上的最大值.
上的最大值.
(Ⅰ)
(Ⅱ)(1)当 时,
时,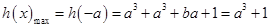
(2)当 时,
时,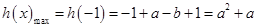
解析试题分析:(Ⅰ)


4分
(Ⅱ)令

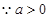
 在
在 ,
, 上单调递增,在
上单调递增,在 上单调递减
上单调递减
又
 (1)当
(1)当 即
即 时,
时,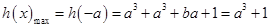
(2)当 即
即 时,
时,
13分
考点:本题主要考查导数的几何意义,直线方程,应用导数研究函数的单调性、最值。
点评:中档题,本题属于导数应用中的基本问题,利用曲线切线的斜率,等于函数在切点的导函数值,建立a,b,c的方程组,达到解题目的。通过研究函数的单调性,明确了最值情况。

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
 的空气隔层.根据热传导知识,对于厚度为
的空气隔层.根据热传导知识,对于厚度为 的均匀介质,两侧的温度差为
的均匀介质,两侧的温度差为 ,单位时间内,在单位面积上通过的热量
,单位时间内,在单位面积上通过的热量 ,其中
,其中 为热传导系数.假定单位时间内,在单位面积上通过每一层玻璃及空气隔层的热量相等.(注:玻璃的热传导系数为
为热传导系数.假定单位时间内,在单位面积上通过每一层玻璃及空气隔层的热量相等.(注:玻璃的热传导系数为 ,空气的热传导系数为
,空气的热传导系数为 .)
.)
 ,
, ,内层玻璃外侧温度为
,内层玻璃外侧温度为 ,外层玻璃内侧温度为
,外层玻璃内侧温度为 ,且
,且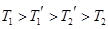 .试分别求出单层玻璃和双层中空玻璃单位时间内,在单位面积上通过的热量(结果用
.试分别求出单层玻璃和双层中空玻璃单位时间内,在单位面积上通过的热量(结果用 (0
(0 x
x 平方米,矩形一边的长为
平方米,矩形一边的长为 米(如图所示)
米(如图所示)
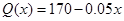 ,试问生产多少件产品,总利润最高?(总利润=总销售额-总的成本)
,试问生产多少件产品,总利润最高?(总利润=总销售额-总的成本)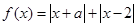
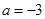 时,求不等式
时,求不等式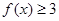 的解集; (2)若
的解集; (2)若 的解集包含
的解集包含 ,求
,求 的取值范围.
的取值范围. 的正方形铁片,铁片的四角截去四个边长均为
的正方形铁片,铁片的四角截去四个边长均为 的小正方形,然后做成一个无盖方盒。
的小正方形,然后做成一个无盖方盒。 表示为
表示为