题目内容
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为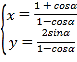 (
(![]() 为参数).以
为参数).以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() ),将曲线
),将曲线![]() 向左平移2个单位长度得到曲线
向左平移2个单位长度得到曲线![]() .
.
(1)求曲线![]() 的普通方程和极坐标方程;
的普通方程和极坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() 的极坐标方程为
的极坐标方程为![]() ,普通方程为
,普通方程为![]() ;(2)
;(2)![]()
【解析】
(1)根据三角函数恒等变换可得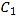 ,
, 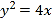 ,可得曲线
,可得曲线![]() 的普通方程,再运用图像的平移得依题意得曲线
的普通方程,再运用图像的平移得依题意得曲线![]() 的普通方程为,利用极坐标与平面直角坐标互化的公式可得方程;
的普通方程为,利用极坐标与平面直角坐标互化的公式可得方程;
(2)法一:将![]() 代入曲线
代入曲线![]() 的极坐标方程得
的极坐标方程得![]() ,运用韦达定理可得
,运用韦达定理可得![]() ,根据
,根据![]() ,可求得
,可求得![]() 的范围;
的范围;
法二:设直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() 为直线的倾斜角),代入曲线
为直线的倾斜角),代入曲线![]() 的普通方程得
的普通方程得![]() ,运用韦达定理可得
,运用韦达定理可得![]() ,根据
,根据![]() ,可求得
,可求得![]() 的范围;
的范围;
(1)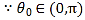 ,
, 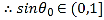
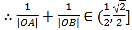 ,即曲线
,即曲线![]() 的普通方程为
的普通方程为![]() ,
,
依题意得曲线![]() 的普通方程为
的普通方程为![]() ,
,
令![]() ,
,![]() 得曲线
得曲线![]() 的极坐标方程为
的极坐标方程为![]() ;
;
(2)法一:将![]() 代入曲线
代入曲线![]() 的极坐标方程得
的极坐标方程得![]() ,则
,则
![]() ,
,![]() ,
,![]() ,
,![]() 异号
异号
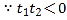 ,
,
![]() ,
,![]() ,
,![]() ;
;
法二:设直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() 为直线的倾斜角),代入曲线
为直线的倾斜角),代入曲线![]() 的普通方程得
的普通方程得![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() 异号
异号
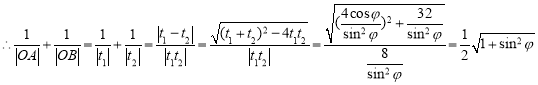
![]() ,
,![]() ,
,![]() .
.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目