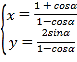题目内容
【题目】在平面直角坐标系![]() 中,点
中,点![]() 到点
到点![]() 的距离比它到
的距离比它到![]() 轴的距离多1,记点
轴的距离多1,记点![]() 的轨迹为
的轨迹为![]() ;
;
(1)求轨迹![]() 的方程;
的方程;
(2)求定点![]() 到轨迹
到轨迹![]() 上任意一点
上任意一点![]() 的距离
的距离![]() 的最小值;
的最小值;
(3)设斜率为![]() 的直线
的直线![]() 过定点
过定点![]() ,求直线
,求直线![]() 与轨迹
与轨迹![]() 恰好有一个公共点,两个公共点,三个公共点时
恰好有一个公共点,两个公共点,三个公共点时![]() 的相应取值范围.
的相应取值范围.
【答案】(1) ![]() ;(2)
;(2) ![]() ;
;
(3) 当![]() 时,直线
时,直线![]() 与轨迹
与轨迹![]() 恰好有一个公共点;
恰好有一个公共点;
当![]() 时, 直线
时, 直线![]() 与轨迹
与轨迹![]() 恰好有两个公共点;
恰好有两个公共点;
当![]() 时, 直线
时, 直线![]() 与轨迹
与轨迹![]() 恰好有三个公共点
恰好有三个公共点
【解析】
(1) 设点![]() ,再根据题意求解关于
,再根据题意求解关于![]() 的方程化简即可.
的方程化简即可.
(2)根据(1)中的轨迹方程,分情况讨论![]() 的最小值即可.
的最小值即可.
(3)根据(1)中的方程![]() ,结合直线过
,结合直线过![]() 分三种情况进行讨论即可.
分三种情况进行讨论即可.
(1)设点![]() ,依题意得
,依题意得![]() ,即
,即![]() ,
,
即![]() .化简整理得
.化简整理得![]() .
.
故点![]() 的轨迹
的轨迹![]() 的方程为
的方程为
(2)在点![]() 的轨迹
的轨迹![]() 中,记
中,记![]() ,
,![]() .
.
设![]() ,当点
,当点![]() 的轨迹在
的轨迹在![]() 上时,
上时,![]()
![]() ,当
,当![]() 时取得最小值.
时取得最小值.
当点![]() 的轨迹在
的轨迹在![]() 上时,
上时, ![]()
综上所述:当![]() 时,即
时,即![]() ,
,![]() .
.
(3) 在点![]() 的轨迹
的轨迹![]() 中,记
中,记![]() ,
,![]() .
.
依题意,可设直线![]() 的方程为
的方程为![]() .
.
由方程组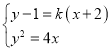 可得
可得![]() ①
①
![]() 当
当![]() 时,此时
时,此时![]() ,把
,把![]() 代入轨迹
代入轨迹![]() 的方程,得
的方程,得![]() .
.
故此时直线![]() :
:![]() 与轨迹
与轨迹![]() 恰好有一个公共点
恰好有一个公共点![]() .
.
![]() 当
当![]() 时,方程①的判别式为
时,方程①的判别式为![]() ②
②
设直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,则
,则
由![]() ,令
,令![]() ,得
,得![]() ③
③
![]() 若
若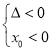 ,由②③解得
,由②③解得![]() ,或
,或![]() .
.
即当![]() 时,直线
时,直线![]() 与
与![]() 没有公共点,与
没有公共点,与![]() 有一个公共点,
有一个公共点,
故此时直线![]() 与轨迹
与轨迹![]() 恰好有一个公共点.
恰好有一个公共点.
![]() 若
若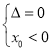 或
或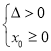 ,由②③解得
,由②③解得![]() ,或
,或![]() .
.
即当![]() 时,直线
时,直线![]() 与
与![]() 只有一个公共点,与
只有一个公共点,与![]() 有一个公共点.
有一个公共点.
当![]() 时, 直线
时, 直线![]() 与
与![]() 有两个公共点,与
有两个公共点,与![]() 没有公共点.
没有公共点.
故当![]() 时,直线
时,直线![]() 与
与![]() 恰好有两个公共点.
恰好有两个公共点.
![]() 若
若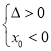 ,由②③解得
,由②③解得![]() ,或
,或![]() .
.
即当![]() 时,直线
时,直线![]() 与
与![]() 有两个公共点,与
有两个公共点,与![]() 有一个公共点,
有一个公共点,
故此时直线![]() 与轨迹
与轨迹![]() 恰好有三个公共点.
恰好有三个公共点.
综上所述:当![]() 时,直线
时,直线![]() 与轨迹
与轨迹![]() 恰好有一个公共点;
恰好有一个公共点;
当![]() 时, 直线
时, 直线![]() 与轨迹
与轨迹![]() 恰好有两个公共点;
恰好有两个公共点;
当![]() 时, 直线
时, 直线![]() 与轨迹
与轨迹![]() 恰好有三个公共点
恰好有三个公共点

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案【题目】某日用品按行业质量标准分成五个等级,等级系数X依次为1,2,3,4,5.现从一批该日用品中随机抽取20件,对其等级系数进行统计分析,得到频率分布表如下:
X | 1 | 2 | 3 | 4 | 5 |
频率 | a | 0.2 | 0.45 | b | c |
(1)若所抽取的20件日用品中,等级系数为4的恰有3件,等级系数为5的恰有2件,求a,b,c的值;
(2)在(1)的条件下,将等级系数为4的3件日用品记为![]() ,等级系数为5的2件日用品记为
,等级系数为5的2件日用品记为![]() ,现从
,现从![]() ,
,![]() 这5件日用品中任取两件(假定每件日用品被取出的可能性相同),求这两件日用品的等级系数恰好相等的概率.
这5件日用品中任取两件(假定每件日用品被取出的可能性相同),求这两件日用品的等级系数恰好相等的概率.