题目内容
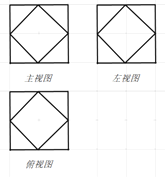
【题目】半正多面体(semiregular solid) 亦称“阿基米德多面体”，是由边数不全相同的正多边形为面的多面体，体现了数学的对称美．二十四等边体就是一种半正多面体，是由正方体切截而成的，它由八个正三角形和六个正方形为面的半正多面体.如图所示，图中网格是边长为1的正方形，粗线部分是某二十四等边体的三视图，则该几何体的体积为（ ）
A.
B.
C.
D.
【答案】D
【解析】
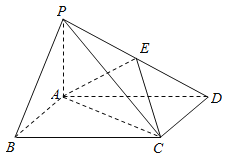
根据三视图作出该二十四等边体如下图所示，求出该几何体的棱长，可以将该几何体看作是相应的正方体沿各棱的中点截去8个三棱锥所得到的，可求出其体积.
如下图所示，将该二十四等边体的直观图置于棱长为2的正方体中，由三视图可知，该几何体的棱长为
，它是由棱长为2的正方体沿各棱中点截去8个三棱锥所得到的，
该几何体的体积为
，
故选：D.
【题目】某日用品按行业质量标准分成五个等级，等级系数X依次为1,2,3,4,5．现从一批该日用品中随机抽取20件，对其等级系数进行统计分析，得到频率分布表如下：
X | 1 | 2 | 3 | 4 | 5 |
频率 | a | 0．2 | 0．45 | b | c |
（1）若所抽取的20件日用品中，等级系数为4的恰有3件，等级系数为5的恰有2件，求a，b，c的值；
（2）在（1）的条件下，将等级系数为4的3件日用品记为
，等级系数为5的2件日用品记为
，现从，这5件日用品中任取两件（假定每件日用品被取出的可能性相同），求这两件日用品的等级系数恰好相等的概率．
【题目】某蛋糕店制作并销售一款蛋糕，制作一个蛋糕成本3元，且以8元的价格出售，若当天卖不完，剩下的则无偿捐献给饲料加工厂。根据以往100天的资料统计，得到如下需求量表。该蛋糕店一天制作了这款蛋糕
个，以
（单位：个，
，
）表示当天的市场需求量，
（单位：元）表示当天出售这款蛋糕获得的利润.
需求量/个 |
|
|
|
|
|
天数 | 15 | 25 | 30 | 20 | 10 |
（1）当
时，若
时获得的利润为
，
时获得的利润为
，试比较和的大小；
（2）当时，根据上表，从利润不少于570元的天数中，按需求量分层抽样抽取6天.
（i）求此时利润关于市场需求量的函数解析式，并求这6天中利润为650元的天数；
（ii）再从这6天中抽取3天做进一步分析，设这3天中利润为650元的天数为
，求随机变量的分布列及数学期望.
