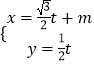题目内容
【题目】[选修4-4：坐标系与参数方程]
已知曲线C的极坐标方程是ρ=4cosθ．以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，直线l的参数方程是：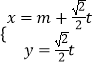 
（t是参数）．
（1）若直线l与曲线C相交于A、B两点，且|AB|= 
，试求实数m值．
（2）设M（x，y）为曲线C上任意一点，求x+2y的取值范围．
【答案】
（1）
解：∵ρ=4cosθ，∴ρ2=4ρcosθ，∴曲线C的直角坐标方程为：x2+y2﹣4x=0，即（x﹣2）2+y2=4．
∵ 
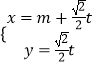，∴直线l的直角坐标方程为：y=x﹣m．即x﹣y﹣m=0．
∵|AB|= 
，∴圆心到直线l的距离（弦心距）d= 
．
即 
，解得m=1或m=3
（2）
解：曲线C的参数方程为： 
（θ为参数），
∵M（x，y）为曲线C上任意一点，∴x+2y=2+2cosθ+4sinθ=2+2 
sin（θ+φ）．
∴x+2y的取值范围是[2﹣2 ，2+2 ]
【解析】（1）求出圆的圆心和半径，根据垂径定理列出方程解出m；（2）求出曲线C的参数方程，将参数方程代入x+2y得到关于参数得三角函数，使用三角函数的性质得出最值．
练习册系列答案
相关题目
