题目内容
【题目】如图,抛物线E:y2=2px(p>0)与圆O:x2+y2=8相交于A,B两点,且点A的横坐标为2.过劣弧AB上动点P(x0 , y0)作圆O的切线交抛物线E于C,D两点,分别以C,D为切点作抛物线E的切线l1 , l2 , l1与l2相交于点M.
(Ⅰ)求p的值;
(Ⅱ)求动点M的轨迹方程.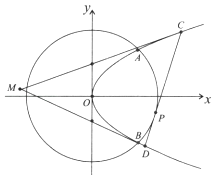
【答案】解:(Ⅰ)由点A的横坐标为2,可得点A的坐标为(2,2),
代入y2=2px,解得p=1,
(Ⅱ)设 ![]() ,
, ![]() ,y1≠0,y2≠0.
,y1≠0,y2≠0.
切线l1: ![]() ,
,
代入y2=2x得 ![]() ,由△=0解得
,由△=0解得 ![]() ,
,
∴l1方程为 ![]() ,同理l2方程为
,同理l2方程为 ![]() ,
,
联立 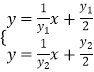 ,解得
,解得  ,
,
∵CD方程为x0x+y0y=8,其中x0 , y0满足 ![]() ,
, ![]() ,
,
联立方程 ![]() 得
得 ![]() ,则
,则 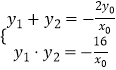 ,
,
代入  可知M(x,y)满足
可知M(x,y)满足  ,
,
代入 ![]() 得
得 ![]() ,
,
考虑到 ![]() ,知
,知 ![]() .
.
∴动点M的轨迹方程为 ![]() ,
, ![]()
【解析】(Ⅰ)由点A的横坐标为2,可得点A的坐标为(2,2),代入y2=2px,解p.(Ⅱ)设 ![]() ,
, ![]() ,y1≠0,y2≠0.切线l1:
,y1≠0,y2≠0.切线l1: ![]() ,代入y2=2x,求出
,代入y2=2x,求出 ![]() ,得到l1方程为
,得到l1方程为 ![]() ,同理l2方程为
,同理l2方程为 ![]() ,联立直线方程组,求出M,利用CD方程为x0x+y0y=8,联立方程
,联立直线方程组,求出M,利用CD方程为x0x+y0y=8,联立方程 ![]() 利用韦达定理,代入
利用韦达定理,代入  可知M(x,y)满足
可知M(x,y)满足  ,求出动点M的轨迹方程.
,求出动点M的轨迹方程.

 名校课堂系列答案
名校课堂系列答案【题目】“女大学生就业难”究竟有多难?其难在何处?女生在求职中是否收到了不公平对待?通过对某大学应届毕业生的调查与实证分析试对下列问题提出解答.为调查某地区大学应届毕业生的调查,用简单随机抽样方法从该地区抽取了500为大学生做问卷调查,结果如下:
性别 | 男 | 女 |
公平 | 40 | 30 |
不公平 | 160 | 270 |
(1)估计该地区大学生中,求职中收到了公平对待的学生的概率;
(2)能否有99%的把握认为该地区的大学生求职中受到了不公平对待与性别有关?
(3)根据(2)的结论,能否提出更好的调查方法来估计该地区的大学生中,求职中是否受到了不公平对待学生的比例?说明理由.
附:K2= ![]()
P(K2≥k) | 0.000 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |

