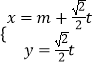题目内容

【题目】我国南宋著名数学家秦九韶发现了从三角形三边求三角形面积的“三斜公式”，设△ABC三个内角A、B、C所对的边分别为a、b、c，面积为S，则“三斜求积”公式为 ．若a2sinC=4sinA，（a+c）2=12+b2 ， 则用“三斜求积”公式求得△ABC的面积为（ ）
A.
B.2
C.3
D.

【答案】A
【解析】解：根据正弦定理：由a2sinC=4sinA得ac=4，则由（a+c）2=12+b2得a2+c2﹣b2=4，则 ． 故选A．
【考点精析】根据题目的已知条件，利用类比推理的相关知识可以得到问题的答案，需要掌握根据两类不同事物之间具有某些类似(或一致)性,推测其中一类事物具有与另外一类事物类似的性质的推理,叫做类比推理．

练习册系列答案
相关题目

【题目】设集合A、B均为实数集R的子集，记：A+B={a+b|a∈A，b∈B}；
（1）已知A={0，1，2}，B={﹣1，3}，试用列举法表示A+B；
（2）设a1= ，当n∈N* ， 且n≥2时，曲线 的焦距为an ， 如果A={a1 ， a2 ， …，an}，B= ，设A+B中的所有元素之和为Sn ， 对于满足m+n=3k，且m≠n的任意正整数m、n、k，不等式Sm+Sn﹣λSk＞0恒成立，求实数λ的最大值；
（3）若整数集合A1A1+A1 ， 则称A1为“自生集”，若任意一个正整数均为整数集合A2的某个非空有限子集中所有元素的和，则称A2为“N*的基底集”，问：是否存在一个整数集合既是自生集又是N*的基底集？请说明理由．

【题目】设向量 =（cosθ，sinθ）， =（﹣ ， ）；
（1）若 ∥ ，且θ∈（0，π），求θ；
（2）若|3 + |=| ﹣3 |，求| + |的值．

【题目】已知O为坐标原点，F是椭圆C： + =1（a＞b＞0）的左焦点，A，B分别为C的左，右顶点．P为C上一点，且PF⊥x轴，过点A的直线l与线段PF交于点M，与y轴交于点E．若直线BM经过OE的中点，则C的离心率为（ ）
A.
B.
C.
D.

【题目】[选修4-4：坐标系与参数方程]

已知曲线C的极坐标方程是ρ=4cosθ．以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，直线l的参数方程是： （t是参数）．
（1）若直线l与曲线C相交于A、B两点，且|AB|= ，试求实数m值．
（2）设M（x，y）为曲线C上任意一点，求x+2y的取值范围．

【题目】已知圆O：x2+y2=1过椭圆C： （a＞b＞0）的短轴端点，P，Q分别是圆O与椭圆C上任意两点，且线段PQ长度的最大值为3． （Ⅰ）求椭圆C的方程；
（Ⅱ）过点（0，t）作圆O的一条切线交椭圆C于M，N两点，求△OMN的面积的最大值．

【题目】某超市从现有甲、乙两种酸奶的日销售量（单位：箱）的1200个数据（数据均在区间（0，50]内）中，按照5%的比例进行分层抽样，统计结果按（0，10]，（10，20]，（20，30]，（30，40]，（40，50]分组，整理如下图：
（Ⅰ）写出频率分布直方图（图乙）中a的值；记所抽取样本中甲种酸奶与乙种酸奶日销售量的方差分别为 ， ，试比较 与 的大小（只需写出结论）；
（Ⅱ）从甲种酸奶日销售量在区间（0，20]的数据样本中抽取3个，记在（0，10]内的数据个数为X，求X的分布列；
（Ⅲ）估计1200个日销售量数据中，数据在区间（0，10]中的个数．

【题目】已知定义在[0，1]上的函数f（x）满足：
①f（0）=f（1）=0；
②对所有x，y∈[0，1]，且x≠y，有|f（x）﹣f（y）|＜ |x﹣y|．
若对所有x，y∈[0，1]，|f（x）﹣f（y）|＜m恒成立，则m的最小值为（ ）
A.
B.
C.
D.

【题目】在平面直角坐标系xOy中，F是抛物线C：x2=2py（p＞0）的焦点，M是抛物线C上位于第一象限内的任意一点，过M，F，O三点的圆的圆心为Q，点Q到抛物线C的准线的距离为 ．
（1）求抛物线C的方程；
（2）是否存在点M，使得直线MQ与抛物线C相切于点M？若存在，求出点M的坐标；若不存在，说明理由；
（3）若点M的横坐标为 ，直线l：y=kx+ 与抛物线C有两个不同的交点A，B，l与圆Q有两个不同的交点D，E，求当 ≤k≤2时，|AB|2+|DE|2的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网