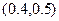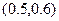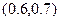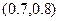题目内容
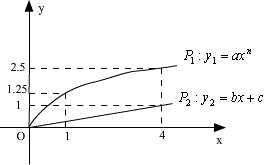
用6.25万元投资甲商品,3.75万元投资乙商品
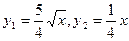 , 4分
, 4分设用x万元投资甲商品,那么投资乙商品为10 -x万元,总利润为y万元..
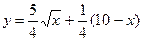 6分
6分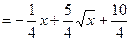
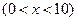 10分
10分当且仅当
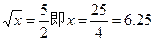 时,
时, 11分
11分答:用6.25万元投资甲商品,3.75万元投资乙商品,才能获得最大利润. 12分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
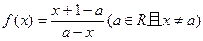
 ,a+1]时,求证:f(x)的值域为[-3,-2];
,a+1]时,求证:f(x)的值域为[-3,-2];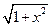 定义在区间[-1,1]上,设x1,x2∈[-1,1]且x1≠x2.
定义在区间[-1,1]上,设x1,x2∈[-1,1]且x1≠x2.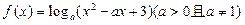 ,满足对任意的
,满足对任意的 、
、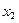 ,当
,当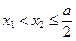 时,
时,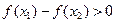 ,则实数
,则实数 的取值范围为( )
的取值范围为( )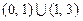
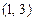
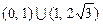
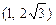
 ,
,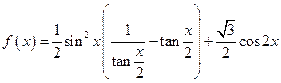 .
.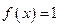 ,求
,求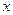 的值.
的值.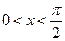 ,求
,求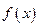 的单调的递减区间;
的单调的递减区间;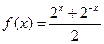
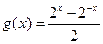
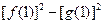 ;
;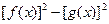 是定值
是定值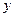 (单位:万元)随销售利润
(单位:万元)随销售利润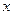 (单位:万元)的增加而增加,但奖金总数不超过
(单位:万元)的增加而增加,但奖金总数不超过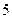 万元,同时奖金不超过利润的
万元,同时奖金不超过利润的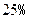 .现有三个奖励模型:
.现有三个奖励模型: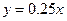 ,
,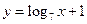 ,
,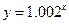 .其中哪个模型能符合公司的要求?
.其中哪个模型能符合公司的要求? ,且
,且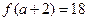 ,
,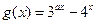 的定义域为[-1,1]。
的定义域为[-1,1]。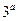 值及函数
值及函数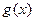 的解析式;
的解析式;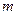 有解,求实数
有解,求实数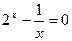 的解所在区间一定是:
的解所在区间一定是: