题目内容
已知函数: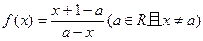
(Ⅰ)证明:f(x)+2+f(2a-x)=0对定义域内的所有x都成立.
(Ⅱ)当f(x)的定义域为[a+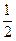 ,a+1]时,求证:f(x)的值域为[-3,-2];
,a+1]时,求证:f(x)的值域为[-3,-2];
(Ⅲ)设函数g(x)=x2+|(x-a)f(x)| ,求g(x) 的最小值 .
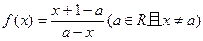
(Ⅰ)证明:f(x)+2+f(2a-x)=0对定义域内的所有x都成立.
(Ⅱ)当f(x)的定义域为[a+
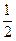 ,a+1]时,求证:f(x)的值域为[-3,-2];
,a+1]时,求证:f(x)的值域为[-3,-2];(Ⅲ)设函数g(x)=x2+|(x-a)f(x)| ,求g(x) 的最小值 .
(Ⅰ)证明见解析
(Ⅱ)证明见解析
(Ⅲ)当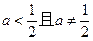 时 g(x)最小值是
时 g(x)最小值是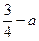
当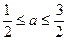 时 g(x)最小值是
时 g(x)最小值是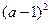 当
当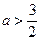 时 g(x)最小值为
时 g(x)最小值为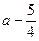
当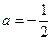 时 g(x)最小值不存在
时 g(x)最小值不存在
(Ⅱ)证明见解析
(Ⅲ)当
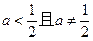 时 g(x)最小值是
时 g(x)最小值是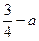
当
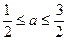 时 g(x)最小值是
时 g(x)最小值是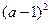 当
当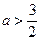 时 g(x)最小值为
时 g(x)最小值为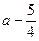
当
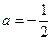 时 g(x)最小值不存在
时 g(x)最小值不存在(Ⅰ)证明: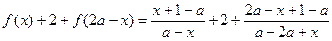
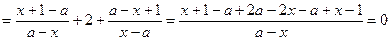
∴结论成立 ……………………………………4分
(Ⅱ)证明:
当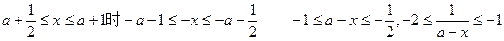
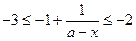 即
即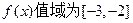 …………9分
…………9分
(Ⅲ)解: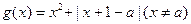
(1)当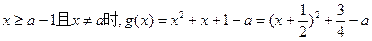
如果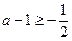 即
即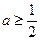 时,则函数在
时,则函数在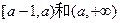 上单调递增
上单调递增
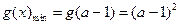
如果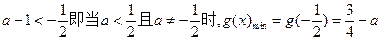
当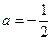 时,
时,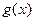 最小值不存在…………………………11分
最小值不存在…………………………11分
(2)当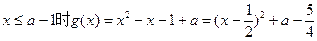
如果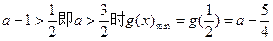
如果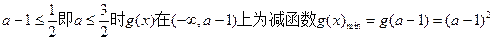
当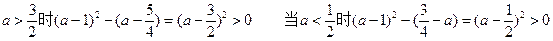
综合得:当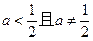 时 g(x)最小值是
时 g(x)最小值是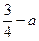
当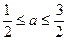 时 g(x)最小值是
时 g(x)最小值是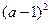 当
当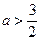 时 g(x)最小值为
时 g(x)最小值为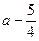
当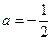 时 g(x)最小值不存在
时 g(x)最小值不存在
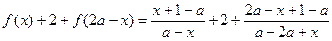
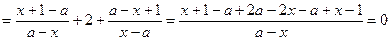
∴结论成立 ……………………………………4分
(Ⅱ)证明:

当
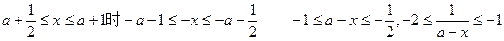
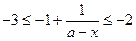 即
即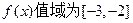 …………9分
…………9分(Ⅲ)解:
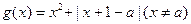
(1)当
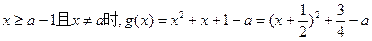
如果
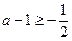 即
即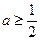 时,则函数在
时,则函数在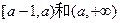 上单调递增
上单调递增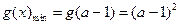
如果
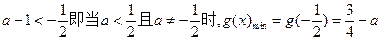
当
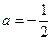 时,
时,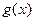 最小值不存在…………………………11分
最小值不存在…………………………11分(2)当
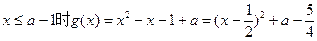
如果
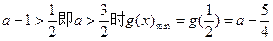
如果
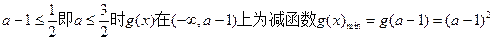
当
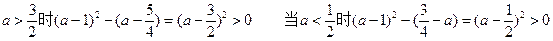
综合得:当
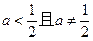 时 g(x)最小值是
时 g(x)最小值是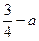
当
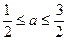 时 g(x)最小值是
时 g(x)最小值是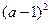 当
当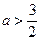 时 g(x)最小值为
时 g(x)最小值为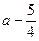
当
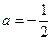 时 g(x)最小值不存在
时 g(x)最小值不存在
练习册系列答案
相关题目
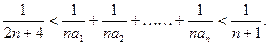
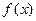 是定义域在
是定义域在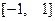 上的奇函数,且其图象上任意两点连线的斜率均小于零.
上的奇函数,且其图象上任意两点连线的斜率均小于零.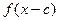 ,
,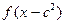 的定义域的交集为空集,求实数
的定义域的交集为空集,求实数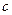 的取值范围;
的取值范围;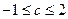 ,则
,则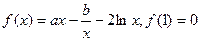 ,
,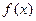 在其定义域内为单调函数,求
在其定义域内为单调函数,求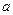 的取值范围;
的取值范围;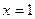 处的切线的斜率为0,且
处的切线的斜率为0,且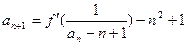 , 已知
, 已知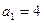 ,求证:
,求证: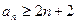
 是
是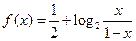 的图象上任意两点,设点
的图象上任意两点,设点 ,且
,且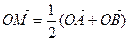 ,若
,若 ,其中
,其中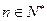 ,且
,且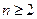 。
。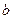 的值;
的值;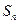 ;
;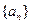 中
中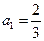 ,当
,当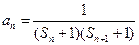 ,设数列
,设数列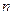 项和为
项和为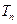 ,
,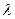 的取值范围使
的取值范围使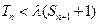 对一切
对一切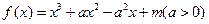 .
.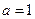 时函数
时函数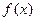 有三个互不相同的零点,求
有三个互不相同的零点,求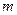 的取值范围;
的取值范围;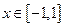 内没有极值点,求
内没有极值点,求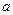 的取值范围;
的取值范围;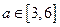 ,不等式
,不等式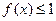 在
在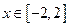 上恒成立,求实数
上恒成立,求实数
 cm,高是
cm,高是 cm.现在以
cm.现在以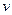 cm
cm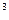 /s的速度向容器内注入某种溶液.求容器内溶液的高度
/s的速度向容器内注入某种溶液.求容器内溶液的高度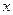 cm与注入溶液的时间
cm与注入溶液的时间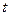 s之间的函数解析式,并写出函数的定义域和值域.
s之间的函数解析式,并写出函数的定义域和值域.