题目内容
已知f(x)=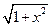 定义在区间[-1,1]上,设x1,x2∈[-1,1]且x1≠x2.
定义在区间[-1,1]上,设x1,x2∈[-1,1]且x1≠x2.
求证: | f(x1)-f(x2)|≤| x1-x2|
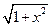 定义在区间[-1,1]上,设x1,x2∈[-1,1]且x1≠x2.
定义在区间[-1,1]上,设x1,x2∈[-1,1]且x1≠x2.求证: | f(x1)-f(x2)|≤| x1-x2|
求证见解析
证
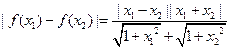

∵
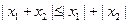 ,
,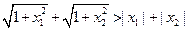 ,
,∴| f(x1)-f(x2)|<| x1-x2| 5分

练习册系列答案
相关题目
题目内容
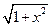 定义在区间[-1,1]上,设x1,x2∈[-1,1]且x1≠x2.
定义在区间[-1,1]上,设x1,x2∈[-1,1]且x1≠x2.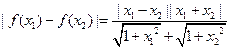

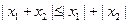 ,
,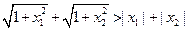 ,
,