题目内容
已知函数 ,且
,且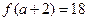 ,
,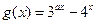 的定义域为[-1,1]。
的定义域为[-1,1]。
1)求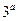 值及函数
值及函数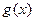 的解析式;
的解析式;
2)若方程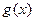 =
=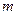 有解,求实数
有解,求实数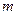 的取值范围。
的取值范围。
 ,且
,且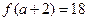 ,
,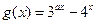 的定义域为[-1,1]。
的定义域为[-1,1]。1)求
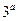 值及函数
值及函数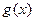 的解析式;
的解析式;2)若方程
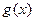 =
=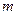 有解,求实数
有解,求实数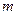 的取值范围。
的取值范围。1)
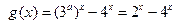 2)
2)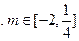
1)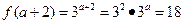
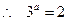
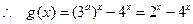 …………5分
…………5分
2)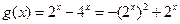 令
令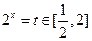
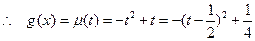 在
在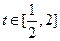 上单调递减
上单调递减
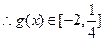
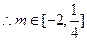 …………14分
…………14分
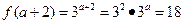
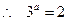
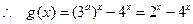 …………5分
…………5分2)
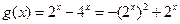 令
令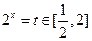
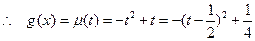 在
在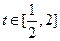 上单调递减
上单调递减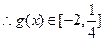
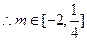 …………14分
…………14分
练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
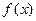 是定义域在
是定义域在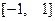 上的奇函数,且其图象上任意两点连线的斜率均小于零.
上的奇函数,且其图象上任意两点连线的斜率均小于零.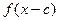 ,
,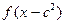 的定义域的交集为空集,求实数
的定义域的交集为空集,求实数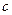 的取值范围;
的取值范围;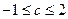 ,则
,则 是
是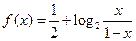 的图象上任意两点,设点
的图象上任意两点,设点 ,且
,且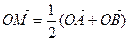 ,若
,若 ,其中
,其中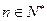 ,且
,且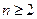 。
。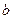 的值;
的值;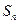 ;
;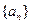 中
中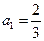 ,当
,当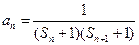 ,设数列
,设数列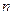 项和为
项和为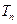 ,
,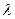 的取值范围使
的取值范围使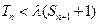 对一切
对一切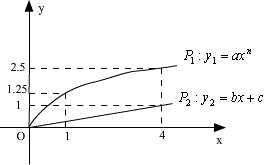
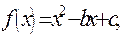 若
若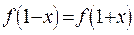 ,且
,且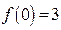 。求
。求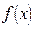
 地10台,
地10台, 地8台.已知从甲地调动1台至
地8台.已知从甲地调动1台至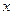 台至
台至 关于台数
关于台数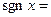
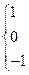
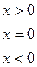 ,则不等式:
,则不等式: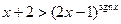 的解集是 .
的解集是 .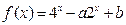 ,当
,当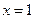 时,
时,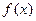 有最小值
有最小值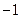 ;
;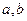 的值; (2)求满足
的值; (2)求满足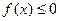 的
的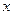 的集合
的集合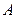 ;
;