题目内容
P为双曲线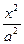 -
-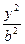 =1(a>0,b>0)上的一点,F1、F2为焦点,若∠F1PF2=60°,则
=1(a>0,b>0)上的一点,F1、F2为焦点,若∠F1PF2=60°,则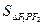 等于( )
等于( )
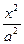 -
-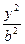 =1(a>0,b>0)上的一点,F1、F2为焦点,若∠F1PF2=60°,则
=1(a>0,b>0)上的一点,F1、F2为焦点,若∠F1PF2=60°,则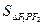 等于( )
等于( )A.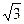 b2 b2 | B.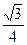 ab ab | C.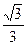 |b2-a2| |b2-a2| | D.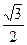 (a2+b2) (a2+b2) |
A
由余弦定理得|PF1|2+|PF2|2-2|PF1|·|PF2|cos60°=4c2,
即|PF1|2+|PF2|2-|PF1||PF2|=4(a2+b2). ①
又由双曲线定义得|PF1|-|PF2|=2a,
∴|PF1|2+|PF2|2-2|PF1||PF2|=4a2. ②
①-②得|PF1||PF2|=4b2,
∴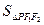 =
=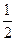 |PF1||PF2|sin
|PF1||PF2|sin =
=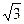 b2.
b2.
即|PF1|2+|PF2|2-|PF1||PF2|=4(a2+b2). ①
又由双曲线定义得|PF1|-|PF2|=2a,
∴|PF1|2+|PF2|2-2|PF1||PF2|=4a2. ②
①-②得|PF1||PF2|=4b2,
∴
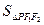 =
=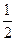 |PF1||PF2|sin
|PF1||PF2|sin =
=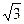 b2.
b2.
练习册系列答案
相关题目
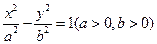 的左、右焦点分别为
的左、右焦点分别为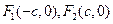 ,若双曲线上存在一点
,若双曲线上存在一点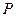 使
使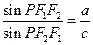 ,则该双曲线的离心率的取值范围是 。
,则该双曲线的离心率的取值范围是 。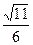 ,且C′的焦距是2
,且C′的焦距是2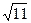 ,则此双曲线的方程为__________________.
,则此双曲线的方程为__________________.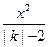 +
+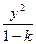 =-1表示焦点在y轴上的双曲线,则它的半焦距c的取值范围是( )
=-1表示焦点在y轴上的双曲线,则它的半焦距c的取值范围是( )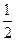 sinA,则顶点A的轨迹方程是( )
sinA,则顶点A的轨迹方程是( )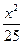 -
-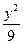 =1和
=1和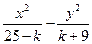 =1(-9<k<25)有( )
=1(-9<k<25)有( )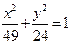 有共同的焦点,且以
有共同的焦点,且以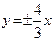 为渐近线.
为渐近线.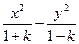 =1表示双曲线,则k的取值范围是( )
=1表示双曲线,则k的取值范围是( )