题目内容
在△ABC中,设内角A,B,C的对边分别为a,b,c向量
=(cosA,sinA),向量
=(
-sinA,cosA),若|
+
|=2.
(1)求角A的大小;
(2)若b=4
,且c=
a,求△ABC的面积.
| m |
| n |
| 2 |
| m |
| n |
(1)求角A的大小;
(2)若b=4
| 2 |
| 2 |
(Ⅰ)∵
+
=(
+cosA-sinA,cosA+sinA)
∴|
+
|2=(
+cosA-sinA)2+(cosA+sinA)2
=2+2
(cosA-sinA)+(cosA-sinA)2+(cosA+sinA)2
=2+2
(cosA-sinA)+2=4-4sin(A-
)
∵|
+
|=2∴4-4sin(A-
)=4sin(A-
)=0
又∵0<A<π∴-
<A-
<
∴A-
=0,
∴A=
(Ⅱ)由余弦定理,a2=b2+c2-2bccosA,又b=4
,c=
a,A=
,得
a2=32+2a2-2×4
×
a•
,
即a2-8
+32=0,解得a=4
∴c=8
∴
=
b•csinA=
×4
×8×sin
=16
=
×(4
)2=16
| m |
| n |
| 2 |
∴|
| m |
| n |
| 2 |
=2+2
| 2 |
=2+2
| 2 |
| π |
| 4 |
∵|
| m |
| n |
| π |
| 4 |
| π |
| 4 |
又∵0<A<π∴-
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
∴A=
| π |
| 4 |
(Ⅱ)由余弦定理,a2=b2+c2-2bccosA,又b=4
| 2 |
| 2 |
| π |
| 4 |
a2=32+2a2-2×4
| 2 |
| 2 |
| ||
| 2 |
即a2-8
| 2a |
| 2 |
∴
| S | △ABC |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| π |
| 4 |
| S | △ABC |
| 1 |
| 2 |
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 满足对任意的
满足对任意的 ,都有
,都有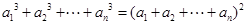 且
且 .
. 的值;
的值; ;
; 的前
的前 项和为
项和为 ,不等式
,不等式 对任意的正整数
对任意的正整数 的取值范围.
的取值范围.
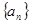 的公差为3,若
的公差为3,若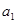 ,
,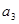 ,
,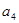 成等比数列,则
成等比数列,则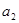 = .
= .