题目内容
如图,在△ABC中,已知点D在BC边上,AD⊥AC,sin∠BAC=
,AB=3
,AD=3,则BD的长为______.

2
| ||
| 3 |
| 2 |

∵AD⊥AC,∴∠DAC=90°,
∴∠BAC=∠BAD+∠DAC=∠BAD+90°,
∴sin∠BAC=sin(∠BAD+90°)=cos∠BAD=
,
在△ABD中,AB=3
,AD=3,
根据余弦定理得:BD2=AB2+AD2-2AB•AD•cos∠BAD=18+9-24=3,
则BD=
.
故答案为:
∴∠BAC=∠BAD+∠DAC=∠BAD+90°,
∴sin∠BAC=sin(∠BAD+90°)=cos∠BAD=
2
| ||
| 3 |
在△ABD中,AB=3
| 2 |
根据余弦定理得:BD2=AB2+AD2-2AB•AD•cos∠BAD=18+9-24=3,
则BD=
| 3 |
故答案为:
| 3 |

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
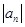 ,
,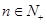 。
。 中,已知
中,已知 ,则
,则 .
.