题目内容
在△ABC中,a,b,c分别为角A,B,C的对边,已知cos2A+6sin2
=4.
(1)求角A的度数;
(2)若a=
,b+c=3,求b、c的值.
| B+C |
| 2 |
(1)求角A的度数;
(2)若a=
| 3 |
(1)∵B+C=π-A,
∴
=
-
,
∴sin
=cos
,
代入已知等式得:cos2A+6cos2
=4,
即2cos2A-1+3(cosA+1)=4,
整理得:2cos2A+3cosA-2=0,
即(2cosA-1)(cosA+2)=0,
∴cosA=
或cosA=-2(舍去),
∵A为三角形内角,∴A=60°;
(2)∵a=
,b+c=3①,cosA=
,
∴由余弦定理得;cosA=
=
=
=
,
整理得:bc=2②,
联立①②解得:b=1,c=2或b=2,c=1.
∴
| B+C |
| 2 |
| π |
| 2 |
| A |
| 2 |
∴sin
| B+C |
| 2 |
| A |
| 2 |
代入已知等式得:cos2A+6cos2
| A |
| 2 |
即2cos2A-1+3(cosA+1)=4,
整理得:2cos2A+3cosA-2=0,
即(2cosA-1)(cosA+2)=0,
∴cosA=
| 1 |
| 2 |
∵A为三角形内角,∴A=60°;
(2)∵a=
| 3 |
| 1 |
| 2 |
∴由余弦定理得;cosA=
| b2+c2-a2 |
| 2bc |
| (b+c)2-a2-2bc |
| 2bc |
| 9-3-2bc |
| 2bc |
| 1 |
| 2 |
整理得:bc=2②,
联立①②解得:b=1,c=2或b=2,c=1.

练习册系列答案
相关题目
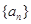 的公差
的公差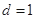 ,前
,前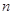 项和为
项和为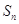 .
.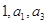 成等比数列,求
成等比数列,求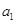 ;(2)若
;(2)若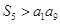 ,求
,求
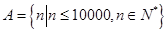 中所有的完全平方数和完全立方数后,将剩下的元素按从
中所有的完全平方数和完全立方数后,将剩下的元素按从