题目内容
一个等比数列的前n项之和是2n-b,那么它的前n项的各项平方之和为( )
| A.(2n-1)2 | B.
| C.4n-1 | D.
|
设该等比数列为{an},前n项和为Sn=2n-b,
则a1=2-b,a2=S2-S1=2,a3=S3-S2=4,
∴22=(2-b)×4,解得b=1,
∴该数列的首项为1,公比为2,
∴an=2n-1,则an2=22n-2,
又
=
=4(常数),
∴{an2}是首项为1,公比为4的等比数列,
∴原等比数列的前n项的各项平方之和为:12+22+42+…+22n-2=
=
(4n-1),
故选D.
则a1=2-b,a2=S2-S1=2,a3=S3-S2=4,
∴22=(2-b)×4,解得b=1,
∴该数列的首项为1,公比为2,
∴an=2n-1,则an2=22n-2,
又
| an+12 |
| an2 |
| 22n |
| 22n-2 |
∴{an2}是首项为1,公比为4的等比数列,
∴原等比数列的前n项的各项平方之和为:12+22+42+…+22n-2=
| 1-4n |
| 1-4 |
| 1 |
| 3 |
故选D.

练习册系列答案
相关题目
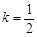 时,数列{an}为递减数列;
时,数列{an}为递减数列;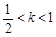 时,数列{an}不一定有最大项;
时,数列{an}不一定有最大项;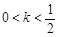 时,数列{an}为递减数列;
时,数列{an}为递减数列;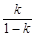 为正整数时,数列{an}必有两项相等的最大项.
为正整数时,数列{an}必有两项相等的最大项. 满足
满足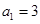 ,
, ,且
,且 ,则
,则