题目内容
10.已知-1,a,b,-4成等差数列,-1,c,d,e,-4成等比数列,则$\frac{b-a}{d}$=( )| A. | $\frac{1}{4}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{2}$或-$\frac{1}{2}$ |
分析 根据等差数列的定义,求出公差d=b-a,根据等比数列即可求出d.
解答 解:∵-1,a,b,-4成等差数列,
∴3(b-a)=-4+1=-3
∴d=b-a=-1
∵-1,c,d,e,-4五个实数成等比数列,
∴d2=(-1)×(-4)=4,d=(-1)q2<0,
∴d=-2,
则$\frac{b-a}{d}$=$\frac{-1}{-2}=\frac{1}{2}$.
故选:B
点评 本题考查等差数列、等比数列的定义,考查学生的计算能力,利用等比数列和等差数列的性质是解决本题的关键.

练习册系列答案
相关题目
3.我市某玩具生产公司根据市场调查分析,决定调整产品生产方案,准备每天生产A,B,C三种玩具共100个,且C玩具至少生产20个.每天生产时间不超过10小时,已知生产这些玩具每个所需工时(分钟)和所获利润如下表:
(1)用每天生产A玩具个数x与B玩具个数y表示每天的利润ω(元)
(2)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
| 玩具名称 | A | B | C |
| 工时(分钟) | 5 | 7 | 4 |
| 利润(元) | 5 | 6 | 3 |
(2)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
18.已知等差数列{an}和{bn}的前n项和分别为Sn,Tn,且$\frac{{S}_{n}}{{T}_{n}}$=$\frac{3n+1}{2n}$,则$\frac{a_5}{b_5}$=( )
| A. | $\frac{8}{5}$ | B. | $\frac{9}{14}$ | C. | $\frac{5}{8}$ | D. | $\frac{14}{9}$ |
20.sin(θ+75°)+cos(θ+45°)-$\sqrt{3}$cos(θ+15°)=( )
| A. | ±1 | B. | 1 | C. | -1 | D. | 0 |
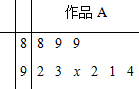 我校开展“爱我河南,爱我方城”摄影比赛,9位评委为参赛作品A给出的分数如茎叶图所示,记分员在去掉一个最高分和一个最低分后,计算的平均分为91,复核员在复核时,发现一个数字(茎叶图中的x)无法看清,若记分员计算无误,则数字x应该是1.
我校开展“爱我河南,爱我方城”摄影比赛,9位评委为参赛作品A给出的分数如茎叶图所示,记分员在去掉一个最高分和一个最低分后,计算的平均分为91,复核员在复核时,发现一个数字(茎叶图中的x)无法看清,若记分员计算无误,则数字x应该是1.