题目内容
3.我市某玩具生产公司根据市场调查分析,决定调整产品生产方案,准备每天生产A,B,C三种玩具共100个,且C玩具至少生产20个.每天生产时间不超过10小时,已知生产这些玩具每个所需工时(分钟)和所获利润如下表:| 玩具名称 | A | B | C |
| 工时(分钟) | 5 | 7 | 4 |
| 利润(元) | 5 | 6 | 3 |
(2)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
分析 (1)依题意,每天生产的玩具C的个数为100-x-y,根据题意即可得出每天的利润;
(II)先根据题意列出约束条件,再根据约束条件画出可行域,设T=2x+3y+300,再利用T的几何意义求最值,只需求出直线z=2x+3y过可行域内的点A时,从而得到T值即可
解答 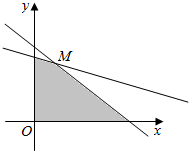 解:(1)由题意ω=5x+6y+3(100-x-y)=2x+3y+300;
解:(1)由题意ω=5x+6y+3(100-x-y)=2x+3y+300;
(2)由题意,约束条件为$\left\{\begin{array}{l}{5x+7y+4(100-x-y)≤600}\\{100-x-y≥20}\\{x≥0}\\{y≥0}\end{array}\right.$
即 $\left\{\begin{array}{l}{x+3y≤200}\\{x+y≤80}\\{x≥0}\\{y≥0}\end{array}\right.$
可行域如图
解方程组$\left\{\begin{array}{l}x+3y=200\\ x+y=80\end{array}\right.$得点M的坐标为(20,60)
所以ωmax=2x+3y+300=520(元)
答:每天生产A玩具20个,B玩具60个,C玩具20个,才能使每天的利润最大,最大利润是520元.
点评 在解决线性规划的应用题时,其步骤为:①分析题目中相关量的关系,列出不等式组,即约束条件,②由约束条件画出可行域,③分析目标函数Z与直线截距之间的关系,④使用平移直线法求出最优解,⑤还原到现实问题中

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
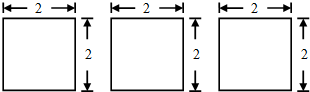
13.若某几何体的三视图 (单位:cm) 如图所示,则此几何体的表面积是(cm2)( )

| A. | 2$\sqrt{13}$π+6 | B. | 2π+6 | C. | $6+(2\sqrt{13}+2)π$ | D. | $6+(\sqrt{13}+2)π$ |
18.不等式2x2-x-1<0的解集为( )
| A. | (-$\frac{1}{2}$,1) | B. | (1,+∞) | C. | (1,2) | D. | (-1,$\frac{1}{2}$) |
9.函数y=x3-3x在(m,6-m2)上有最小值,则实数m的取值范围是( )
| A. | (-$\sqrt{5}$,1) | B. | [-$\sqrt{5}$,1) | C. | [-2,1) | D. | (-2,1) |
10.已知-1,a,b,-4成等差数列,-1,c,d,e,-4成等比数列,则$\frac{b-a}{d}$=( )
| A. | $\frac{1}{4}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{2}$或-$\frac{1}{2}$ |